
【题目】如图,在矩形ABCD中,E是AD上一点,PQ垂直平分BE,分别交AD、BE、BC于点P、O、Q,连接BP、EQ.
(1)求证:四边形BPEQ是菱形;
(2)若AB=6,F为AB的中点,OF+OB=9,求PQ的长.

【答案】(1)证明见解析;(2)PQ的长是![]() .
.
【解析】试题分析:⑴先根据线段垂直平分线的性质证明QB=QE,由ASA证明△BOQ≌△EOP,得出PE=QB,证出四边形ABGE是平行四边形,再根据菱形的判定即可得出结论.
⑵根据三角形中位线的性质可得![]() ,设
,设![]() ,则
,则
![]() ,在Rt△ABE中,根据勾股定理可得
,在Rt△ABE中,根据勾股定理可得![]() ,解得BE=10,
,解得BE=10,
得到![]() ,设
,设![]() ,则
,则![]() ,
, ![]() ,计算得出
,计算得出![]() ,在Rt△BOP中,根据勾股定理可得
,在Rt△BOP中,根据勾股定理可得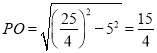 ,由
,由![]() 即可求解.
即可求解.
试题解析:
(1)证明:∵ PQ垂直平分BE,
∴ QB=QE,OB=OE,
∵ 四边形ABCD是矩形,
∴ AD∥BC,
∴ ∠ PEO=∠ QBO,
在△ BOQ与△ EOP中,
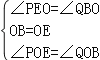 ,
,
∴ △ BOQ≌ △ EOP(ASA),
∴ PE=QB,
又∵ AD∥BC,
∴ 四边形BPEQ是平行四边形,
又∵ QB=QE,
∴ 四边形BPEQ是菱形;
(2)解:∵ O,F分别为PQ,AB的中点,
∴ AE+BE=2OF+2OB=18,
设AE=x,则BE=18﹣x,
在Rt△ ABE中,62+x2=(18﹣x)2,
解得x=8,
BE=18﹣x=10,
∴ OB=![]() BE=5,
BE=5,
设PE=y,则AP=8﹣y,BP=PE=y,
在Rt△ ABP中,62+(8﹣y)2=y2,解得y=![]() ,
,
在Rt△ BOP中,PO=![]() =
=![]() ,
,
∴ PQ=2PO=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知E是ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F,连接AC、BF,若EF=EC,试判断四边形ABFC是什么四边形,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波位于东南沿海,中国大陆海岸线中段,陆域总面积约为9816平方公里.其中9816用科学记数法表示为( )
A.918.6×10B.91.86×102C.9.186×103D.0.9186×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=kx+b与抛物线y=ax2(a>0)相交于A、B两点(点A在点B的左侧),与y轴正半轴相交于点C,过点A作AD⊥x轴,垂足为D.
(1)若∠AOB=60°,AB∥x轴,AB=2,求a的值;
(2)若∠AOB=90°,点A的横坐标为﹣4,AC=4BC,求点B的坐标;
(3)延长AD、BO相交于点E,求证:DE=CO.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系呢?
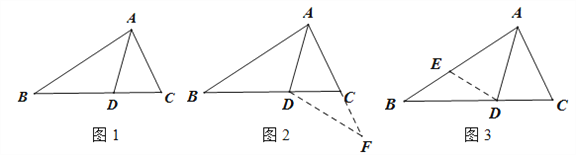
(1)通过观察、实验提出猜想:∠ACB与∠ABC的数量关系,用等式表示为: .
(2)小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:如图2,延长AC到F,使CF=CD,连接DF.通过三角形全等、三角形的性质等知识进行推理,就可以得到∠ACB与∠ABC的数量关系.
想法2:在AB上取一点E,使AE=AC,连接ED,通过三角形全等、三角形的性质等知识进行推理,就可以得到∠ACB与∠ABC的数量关系.
请你参考上面的想法,帮助小明证明猜想中∠ACB与∠ABC的数量关系(一种方法即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com