
【题目】如图,直线AB与CD相交于O.OF是∠BOD的平分线,OE⊥OF.
(1)若∠BOE比∠DOF大38°,求∠DOF和∠AOC的度数;
(2)试问∠COE与∠BOE之间有怎样的大小关系?请说明理由.
(3)∠BOE的余角是 ,∠BOE的补角是 .
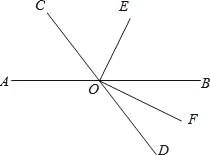
【答案】(1)∠DOF=26°,∠AOC=52°;(2)∠COE=∠BOE;(3)∠BOF和∠DOF,∠AOE和∠DOE.
【解析】试题分析:(1)设∠BOF=α,根据角平分线的定义得出∠DOF=∠BOF=α,得出方程38°+α+α+α=90°,求出方程的解即可;
(2)求出∠COE=180°-∠DOE=90°-∠DOF,根据垂直求出∠BOE=90°-∠BOF,即可得出答案;
(3)根据余角和补角定义求出即可.
试题解析:(1)设∠BOF=α,
∵OF是∠BOD的平分线,
∴∠DOF=∠BOF=α,
∵∠BOE比∠DOF大38°,
∴∠BOE=38°+∠DOF=38°+α,
∵OE⊥OF,
∴∠EOF=90°,
∴38°+α+α+α=90°,
解得:α=26°,
∴∠DOF=26°,∠AOC=∠BOD=∠DOF+∠BOF=26°+26°=52°;
(2)∠COE=∠BOE,
理由是:∵∠COE=180°﹣∠DOE=180°﹣(90°+∠DOF)=90°﹣∠DOF,
∵OF是∠BOD的平分线,
∴∠DOF=∠BOF,
∴∠COE=90°﹣∠BOF,
∵OE⊥OF,
∴∠EOF=90°,
∴∠BOE=90°﹣∠BOF,
∴∠COE=∠BOE;
(3)∠BOE的余角是∠BOF和∠DOF,∠BOE的补角是∠AOE和∠DOE,
故答案为:∠BOF和∠DOF,∠AOE和∠DOE.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.任意购买一张电影票,座号是“7排8号”B.射击运动员射击一次,恰好命中靶心
C.抛掷一枚图钉,钉尖触地D.13名同学中,至少2人出生的月份相同
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M、N分别是AE、CD的中点,判断BM与BN的关系,并说明理由. 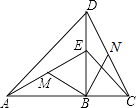
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释正确的是( )
A.线段可以比较大小
B.线段有两个端点
C.两点之间线段最短
D.过两点有且只有一条直线
查看答案和解析>>
科目:初中数学 来源: 题型:
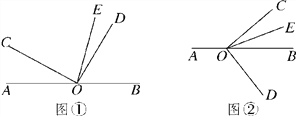
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线CP是AB的中垂线且交AB于P,其中AP=2CP.甲、乙两人想在AB上取两点D、E,使得AD=DC=CE=EB,其作法如下: 甲:作∠ACP、∠BCP之角平分线,分别交AB于D、E,则D、E即为所求;
乙:作AC、BC之中垂线,分别交AB于D、E,则D、E即为所求.
对于甲、乙两人的作法,下列判断何者正确( )
A.两人都正确
B.两人都错误
C.甲正确,乙错误
D.甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠1=18°18′,∠2=18.18°,∠3=18.3°,下列结论正确的是( )
A.∠1=∠3
B.∠1=∠2
C.∠2=∠3
D.∠1=∠2=∠3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com