阅读快车系列答案科目：初中数学 来源： 题型：
对于两个正实数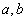
，由于
，所以
，即
，所以得到
，并且当
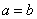时，
．
阅读材料2：
若
，则
，因为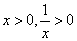
，所以由阅读材料1可得，
，即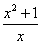
的最小值是2，只有
时，即
时取得最小值．
根据以上阅读材料，请回答以下问题：
（1）比较大小：
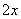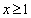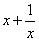
（其中
）； 
（其中
）
（2）已知代数式
变形为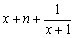
，求常数n的值；
（3）当
时，
有最小值，最小值为 . （直接写出答案）
查看答案和解析>>
科目：初中数学 来源： 题型：
甲、乙两人玩扑克牌游戏，游戏规则是：从牌面数字分别为5、6、7的三张扑克牌中，随机抽取一张，放回后，再随机抽取一张，若所抽的两张牌面数字的积为奇数，则甲获胜；若所抽取的两张牌面数字的积为偶数，则乙获胜，这个游戏___________.（填“公平”或“不公平”）
查看答案和解析>>
科目：初中数学 来源： 题型：
小颖和小红两名同学在学习“概率”时，做投掷骰子（质地均匀的正方体）实验，他们共做了60次实验，实验的结果如下：
| 朝上的点 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现的次数 | 7 | 9 | 6 | 8 | 20 | 10 |
（1）计算“3点朝上”的频率和“5点朝上”的频率.
（2）小颖说：“根据上述实验，一次实验中出现5点朝上的概率最大”；小红说：“如果投
掷600次，那么出现6点朝上的次数正好是100次”.小颖和小红的说法正确吗？为什么？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
的解集为
，那么
的值等于_______.
解析：解不等式组 
可得解集为
，
，
，
，所以
．
的解集为
，则
的值为（ ）
B.
C.2 D.4
相交于点
，
∥
．若 
，则∠
等于（ ）
与
的大小．
于点
，
于点
，
．请问：
平分
吗？若平分，请说明理由．
的不等式组
的解集为
，则
的值分别为___________.
数