
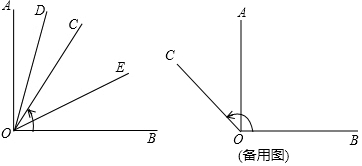
分析 (1)根据角平分线的定义,OD、OE分别平分∠AOC和∠BOC,则可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)①结合角的特点,∠DOE=∠DOC+∠COE,求得结果进行判断和计算;②分三种情况讨论:当90°<n≤180°时,当180°<n≤270°时,当270°<n<360°,分别求得∠DOE的度数;
(3)根据(2)中方法进行分类讨论,即可得出∠DOE的度数.
解答 解:(1)∵OD、OE分别平分∠AOC和∠BOC,
∴∠COE=$\frac{1}{2}$∠COB=30°,∠COD=$\frac{1}{2}$∠AOC=15°,
∴∠DOE=∠COE+∠COD=45°;
故答案为:45°;
(2)①∠DOE的大小不变,等于45°,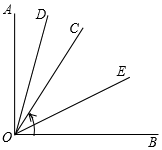
理由:∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠DOC+∠COE
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠AOC+∠BOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°;
②分三种情况: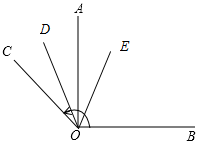
当90°<n≤180°时,∠DOE的大小不变,等于45°,
理由:如图所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠COE-∠DOC
=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC-∠AOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°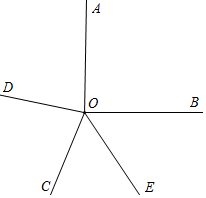
=45°;
当180°<n≤270°时,∠DOE的大小不变,等于135°,
理由:如图所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠COE+∠DOC
=$\frac{1}{2}$∠BOC+$\frac{1}{2}$∠AOC
=$\frac{1}{2}$(∠BOC+∠AOC)
=$\frac{1}{2}$(360°-∠AOB)
=$\frac{1}{2}$×270°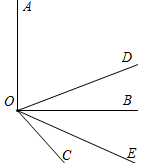
=135°;
当270°<n<360°时,∠DOE的大小不变,等于45°,
理由:如图所示,∵OD平分∠AOC,OE平分∠BOC,
∴∠DOE=∠DOC-∠COE
=$\frac{1}{2}$∠AOC-$\frac{1}{2}$∠BOC
=$\frac{1}{2}$(∠AOC-∠BOC)
=$\frac{1}{2}$∠AOB
=$\frac{1}{2}$×90°
=45°;
(3)在射线OC旋转过程中,∠DOE的度数为$\frac{1}{2}$a或180°-$\frac{1}{2}$a.
理由:当0<n≤180°时,∠DOE=$\frac{1}{2}$a;
当180°<n≤180°+a时,∠DOE=180°-$\frac{1}{2}$a;
当180°+a<n<360°时,∠DOE=$\frac{1}{2}$a;
综上所述,∠DOE的度数为$\frac{1}{2}$a或180°-$\frac{1}{2}$a.
点评 本题主要考查了角的和差关系的运用以及角平分线的定义的运用,即从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.解决问题的关键是画出图形进行分类讨论,分类时注意不能遗漏,也不能重复.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | 0.358×105 | B. | 3.58×104 | C. | 35.8×103 | D. | 358×102 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC≌△DEF,点B与点E是对应点,点A与点D是对应点,下列说法不一定成立的是( )
如图,已知△ABC≌△DEF,点B与点E是对应点,点A与点D是对应点,下列说法不一定成立的是( )| A. | AB=DE | B. | AC=DF | C. | BE=EC | D. | BE=CF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=1}\\{y=0}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
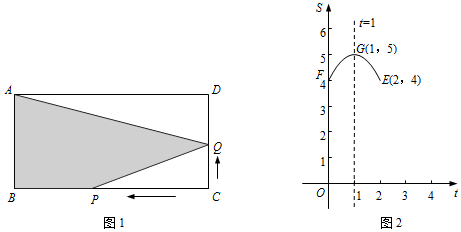
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com