在Rt△ABC中,∠C=90゜,AC=5,BC=12,以C为圆心,R为半径作圆与斜边AB相切,求R的值.
分析:R的长即为斜边AB上的高,由勾股定理易求得AB的长,根据直角三角形面积的不同表示方法,即可求出R的值.
解答: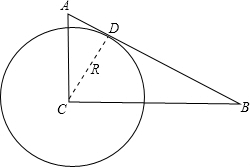
解:Rt△ABC中,∠C=90°,AC=5,BC=12;
由勾股定理,得:AB
2=5
2+12
2=169,
∴AB=13;
∵S
△ABC=
AC•BC=
AB•R;
∴R=
=
.
点评:本题考查的知识点有:切线的性质、勾股定理、直角三角形面积的求法;斜边上的高即为圆的半径是本题的突破点.
