
【题目】如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.
(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
【答案】
(1)
解:连接ME,设MN交BE于P,根据题意,得
MB=ME,MN⊥BE.(2分)
过N作AB的垂线交AB于F.
在Rt△MBP中,∠MBP+∠BMN=90°,
在Rt△MNF中,∠FNM+∠BMN=90°,
∴∠MBP=∠MNF.
在Rt△EBA与Rt△MNF中,
∵AB=FN,
∴Rt△EBA≌Rt△MNF,故MF=AE=x.
在Rt△AME中,AE=x,ME=MB=AB-AM=2-AM,
∴(2-AM)2=x2+AM2.
4-4AM+AM2=x2+AM2,即4-4AM=x2,
解得AM=1- ![]() x2.
x2.
所以梯形ADNM的面积S= ![]() ×AD=
×AD= ![]() ×2
×2
=AM+AF=AM+AM+MF=2AM+AE=2(1- ![]() x2)+x=-
x2)+x=- ![]() x2+x+2
x2+x+2
即所求关系式为s=- ![]() x2+x+2.
x2+x+2.
(2)
解:s=- ![]() x2+x+2=-
x2+x+2=- ![]() (x2-2x+1)+
(x2-2x+1)+ ![]() =-
=- ![]() (x-1)2+
(x-1)2+ ![]()
故当AE=x=1时,四边形ADNM的面积S的值最大,最大值是 ![]() .
.
【解析】(1)通过做辅助线构造全等三角形,利用勾股定理整理出相应的关系式,利用梯形的面积公式来解决问题.(2)注意对二次函数解析式整理时用顶点式进行整理简单


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在△ABC 中,∠A=90°,AB=AC=![]() +1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
+1,P 是△ABC 内一个动点,PD⊥AB、PE⊥AC、PF⊥BC,垂足分别为 D、E、F,且 PD+PE=PF.则点 P 运动所形成的图形的长度是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
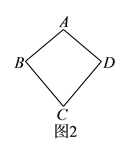
【题目】从图![]() 所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
具体定义如下:如图![]() ,在四边形
,在四边形![]() 中,
中, ![]() ,
, ![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.
,我们把这种两组邻边分别相等的四边形叫做“筝形”.

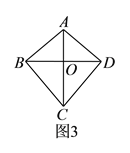
(![]() )结合图
)结合图![]() ,通过观察、测量、折纸,可以猜想“筝形”具有诸如“
,通过观察、测量、折纸,可以猜想“筝形”具有诸如“![]() 平分
平分![]() 和
和![]() ”这样的性质,请结合图形,再写出两条“筝形”的性质.
”这样的性质,请结合图形,再写出两条“筝形”的性质.
①____________________________.
②____________________________.
(![]() )从你写出的两条性质中,任选一条“筝形”的性质给出证明.
)从你写出的两条性质中,任选一条“筝形”的性质给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在如图所示的平面直角中, 将其平移后得△![]() , 若B的对应点
, 若B的对应点![]() 的坐标是(-2, 2).
的坐标是(-2, 2).
(1) 在图中画出△![]() ;
;
(2) 此次平移可看作将△ABC向_____平移了____个单位长度, 再向___平移了___个单位长度得△![]() ;
;
(3) △ABC的面积为____________.(△ABC的面积可以看作一个长方形的面积减去一些小三角形的面积)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究 探索:在如图1至图3中,△ABC的面积为a .
(1)如图1, 延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1,则S1=________(用含a的代数式表示);




(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2,则S2= (用含a的代数式表示);
(3)在图2的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=__________(用含a的代数式表示).
发现:像上面那样,将△ABC各边均顺次延长一倍,连结所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,函数y=-x2+bx+c的部分图象与x轴、y轴的交点分别为A(1,0),B(0,3),对称轴是x=-1,在下列结论中,错误的是( )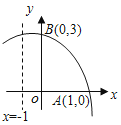
A.顶点坐标为(-1,4)
B.函数的解析式为y=-x2-2x+3
C.当x<0时,y随x的增大而增大
D.抛物线与x轴的另一个交点是(-3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x-2)(x-3)=m有实数根x1、x2 , 且x1≠x2 , 有下列结论:①x1=2,x2=3;②m> ![]() ;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )
;③二次函数y=(x-x1)(x-x2)+m的图象与x轴交点的坐标为(2,0)和(3,0).其中,正确结论的个数是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图.

(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差;
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com