
分析 首先根据根的情况利用根的判别式解得a的取值范围,然后根据根两个不相等的实数根都在-1和0之间(不包括-1和0),结合函数图象确定其函数值的取值范围得a,易得a的取值范围.
解答 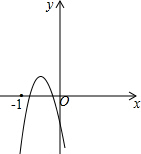 解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根
解:∵关于x的一元二次方程ax2-3x-1=0的两个不相等的实数根
∴△=(-3)2-4×a×(-1)>0,
解得:a>$-\frac{9}{4}$
设f(x)=ax2-3x-1,如图,
∵实数根都在-1和0之间,
∴-1$<-\frac{-3}{2a}<0$,
∴a$<-\frac{3}{2}$,
且有f(-1)<0,f(0)<0,
即f(-1)=a×(-1)2-3×(-1)-1<0,f(0)=-1<0,
解得:a<-2,
∴$-\frac{9}{4}$<a<-2,
故答案为:$-\frac{9}{4}$<a<-2.
点评 本题主要考查了一元二次方程根的情况的判别及抛物线与x轴的交点,数形结合确定当x=0和当x=-1时函数值的取值范围是解答此题的关键.


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:填空题
| 候选人 | 甲 | 乙 | 丙 | 丁 | |
| 测试成绩(百分制) | 面试 | 86 | 92 | 90 | 83 |
| 笔试 | 90 | 83 | 83 | 92 | |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.81×10-9米 | B. | 0.81×10-8米 | C. | 8.1×10-7米 | D. | 8.1×10-9米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 15 | C. | 18 | D. | 21 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.1×10-12 | B. | 1.1×10-13 | C. | 11×10-12 | D. | 11×10-13 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com