
【题目】如图:在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数6,
点表示数6,
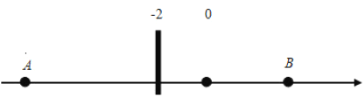
(1)A、B两点之间的距离等于_________;
(2)在数轴上有一个动点![]() ,它表示的数是
,它表示的数是![]() ,则
,则![]() 的最小值是_________;
的最小值是_________;
(3)若点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,请在数轴上找一点
,请在数轴上找一点![]() ,使
,使![]() ,则
,则![]() 点表示的数是_________;
点表示的数是_________;
(4)若在原点![]() 的左边2个单位处放一挡板,一小球甲从点
的左边2个单位处放一挡板,一小球甲从点![]() 处以5个单位/秒的速度向右运动;同时另一小球乙从点
处以5个单位/秒的速度向右运动;同时另一小球乙从点![]() 处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为
处以2个单位/秒的速度向左运动,在碰到挡板后(忽略球的大小,可看作一点)两球分别以原来的速度向相反的方向运动,设运动时间为![]() 秒,请用
秒,请用![]() 来表示甲、乙两小球之间的距离
来表示甲、乙两小球之间的距离![]() .
.
【答案】(1)16 (2)16 (3)2或14 (4)甲、乙两小球之间的距离![]() 为:
为:![]() 或
或![]() ,或
,或![]() .
.
【解析】
(1)根据数轴上两点之间的距离公式计算即可;
(2)先根据P点在数轴上的位置分类讨论,然后求最小值即可;
(3)由题意可知:点C距离B点较近,设点C所表示的数为y,然后根据点C与点B的位置分类讨论即可;
(4)根据题意:点A到表示﹣2的点的距离为:﹣2-(﹣10)=8,点B到表示﹣2的点的距离为:6-(﹣2)=8,甲球从A到﹣2所需时间为:8÷5=![]() s,乙球从B到﹣2所需时间为:8÷2=4s,然后用t分别表示出甲球从点A到表示﹣2的点之前和之后,甲球所表示的数,乙球从点B到表示﹣2的点之前和之后,乙球所表示的数,根据数轴上两点之间的距离公式,即可求出甲乙两球的距离.
s,乙球从B到﹣2所需时间为:8÷2=4s,然后用t分别表示出甲球从点A到表示﹣2的点之前和之后,甲球所表示的数,乙球从点B到表示﹣2的点之前和之后,乙球所表示的数,根据数轴上两点之间的距离公式,即可求出甲乙两球的距离.
解:(1)![]()
故答案为:16;
(2)根据数轴上两点的距离公式可知:![]() 表示点P与点A之间的距离,
表示点P与点A之间的距离,![]() 表示点P与点B之间的距离
表示点P与点B之间的距离
①若点P在A点左侧时,即x<﹣10,由下图可知:PB>AB=16,即![]()
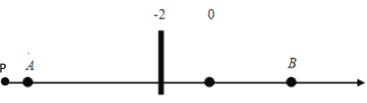
∴此时![]() ;
;
②若点P在线段AB上时,即﹣10≤x≤6,由下图可知:PA+PB=AB=16,
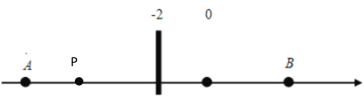
∴此时![]() ;
;
③若点P在B点右侧时,即x>6,由下图可知:PA>AB=16,即![]()
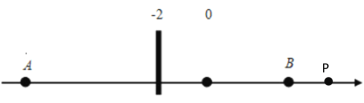
∴此时![]() ;
;
综上所述:![]() (当点P在线段AB上时,即﹣10≤x≤6,取等号)
(当点P在线段AB上时,即﹣10≤x≤6,取等号)
∴![]() 的最小值是16;
的最小值是16;
故答案为:16.
(3)∵![]()
∴点C距离B点较近
设点C所表示的数为y
①当C在B点左侧时,如下图所示,
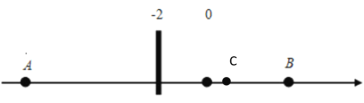
∴AC=y-(﹣10)=y+10,BC=6-y
∵![]()
∴y+10=3(6-y)
解得:y=2;
②当C在B点右侧时,如下图所示,
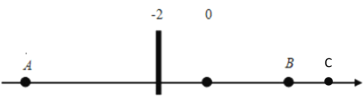
∴AC=y-(﹣10)=y+10,BC= y -6
∵![]()
∴y+10=3(y -6)
解得:y=14.
综上所述:![]() 点表示的数是2或14.
点表示的数是2或14.
(4)点A到表示﹣2的点的距离为:﹣2-(﹣10)=8,点B到表示﹣2的点的距离为:6-(﹣2)=8,甲球从A到﹣2所需时间为:8÷5=![]() s,乙球从B到﹣2所需时间为:8÷2=4s,
s,乙球从B到﹣2所需时间为:8÷2=4s,
∴运动![]() 秒钟后,甲球表示的数是:
秒钟后,甲球表示的数是:![]() 或
或![]() ;
;
乙球表示的数是:![]() 或
或![]() ,
,
∴![]() 或
或![]() ,或
,或![]() .
.
∴甲、乙两小球之间的距离![]() 为:
为:![]() 或
或![]() ,或
,或![]() .
.


科目:初中数学 来源: 题型:
【题目】有3张纸牌,分別是红桃3、红桃4和黑桃5(简称红3,红4,黑5).把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.
(1)两次抽得纸牌均为红桃的概率;(请用“画树状图”或“列表”等方法写出分析过程)
(2)甲、乙两人做游戏,现有两种方案.A方案:若两次抽得花色相同则甲胜,否则乙胜.B方案:若两次抽得纸牌的数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
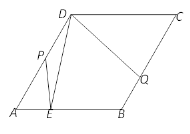
【题目】如图,在菱形![]() 中,
中,![]() =60°, AB=2,点E是AB上的动点,作∠EDQ=60°交BC于点Q,点P在AD上,PD=PE.
=60°, AB=2,点E是AB上的动点,作∠EDQ=60°交BC于点Q,点P在AD上,PD=PE.
(1)求证:AE=BQ;
(2)连接PQ, EQ,当∠PEQ=90°时,求![]() 的值;
的值;
(3)当AE为何值时,△PEQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产150辆自行车,平均每天生产辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产 辆;
(2)产量最多的一天比生产量最少的一天多生产 辆;
(3)该厂实行计划工资制,每辆车![]() 元,超额完成任务每辆奖
元,超额完成任务每辆奖![]() 元,少生产一辆扣
元,少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少?
元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
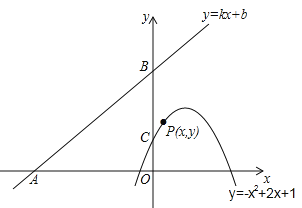
A. 1.4 B. 2.5 C. 2.8 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上任意两点之间的距离均可用“右﹣左”表示,即右边的数(较大)减去左边的数(较小).已知数轴上两点A、B对应的数分别为﹣2、5,则A、B两点之间的距离记为AB,且AB=5﹣(﹣2)=7.P为数轴上的动点,其对应的数为x.
![]()
(1)若点P到A,B两点的距离相等,写出点P对应的数;
(2)数轴上是否存在点P,使点P到A,B两点的距离之和为11,若存在,请求出x的值;若不存在,请说明理由;
(3)若点P在原点,现在A,B,P三个点均向左匀速运动,其中点P的速度为每秒1个单位;A,B两点中有一个点速度与点P的速度一致,另一个点以每秒3单位的速度运动;则几秒后点P到A,B两点的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC=CD=AD=4,∠DAB=∠B=∠C=∠D=90°,E,F分别是边BC,CD上的点,且CE=![]() BC,F为CD的中点,问△AEF是什么三角形?请说明理由.
BC,F为CD的中点,问△AEF是什么三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(![]() -
-![]() +
+![]() )×36]÷5 (4)99
)×36]÷5 (4)99![]() ×(-36)
×(-36)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com