
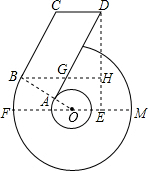
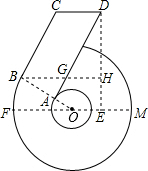
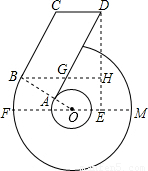
已知“6”字形图中,FM是大⊙O的直径, BC与大⊙O相切于B, OB与小⊙O相交于A, AD∥BC,CD∥BH∥FM, DH⊥BH于H,设∠FOB=30°,OB=4, BC=6.
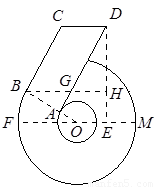
﹙1﹚求证:AD为小⊙O的切线;
﹙2﹚求DH的长.﹙结果保留根号﹚
(1)证明见解析(2) 
【解析】(1)证明:∵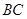 是大⊙O的切线,∴∠
是大⊙O的切线,∴∠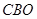 =90°.
=90°.
∵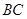 ∥
∥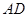 , ∴∠BAD=90°.即
, ∴∠BAD=90°.即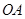 ⊥
⊥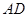 .
.
又∵点A在小⊙O上,∴AD是小⊙O的切线. ············· 2分
(2)∵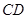 ∥
∥ ,
,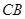 ∥
∥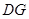 ,∴四边形
,∴四边形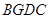 是平行四边形.
是平行四边形.
∴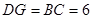 . ························· 3分
. ························· 3分
∵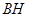 ∥
∥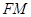 ,∴
,∴ .
.
∴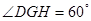 .
.
又∵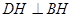 ,
,
∴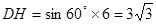 . 5分
. 5分
(1)证OA⊥AD即可.由BC与大⊙O相切于B,得OB⊥BC;AD∥BC,则OB⊥AD.得证.
(2)易证四边形BCDG是平行四边形,则DG=BC=6;由∠FOB=30°,BH∥FM可得∠OBG=30°,∠BGA=60°=∠DGH.在Rt△DGH中运用三角函数求解.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2012年江西抚州市崇仁四中初三第二次月考数学试卷(带解析) 题型:解答题
已知“6”字形图中,FM是大⊙O的直径, BC与大⊙O相切于B, OB与小⊙O相交于A, AD∥BC,CD∥BH∥FM, DH⊥BH于H,设∠FOB=30°,OB="4," BC=6.
﹙1﹚求证:AD为小⊙O的切线;
﹙2﹚求DH的长.﹙结果保留根号﹚
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第5章《中心对称图形(二)》中考题集(39):5.5 直线与圆的位置关系(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com