
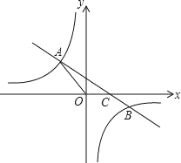
【题目】如图,一次函数y=kx+b(k≠0)的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(﹣2,3),点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使△APC是直角三角形?若存,求出点P的坐标;若不存在,请说明理由.
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△OAC中,∠OCA=90°,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=![]() (k>0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若∠A=∠COD,则直线OA的解析式为______.
(k>0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若∠A=∠COD,则直线OA的解析式为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
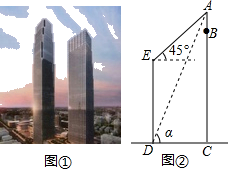
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
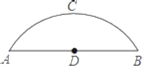
【题目】如图,有一座圆弧形拱桥,桥下水面宽度AB为12m,拱高CD为4m.
(1)求拱桥的半径;
(2)有一艘宽5m的货船,船舱顶部为长方形,并高出水面3.6m,求此货船是否能顺利通过拱桥?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数,反比例函数或二次函数中的一种)
x(亩) | 20 | 25 | 30 | 35 |
y(元) | 1800 | 1700 | 1600 | 1500 |
(1)请求出种植樱桃的面积超过15亩时每亩获得利润y与x的函数关系式;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过50亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,四边形
轴的正半轴上,四边形![]() 是平行四边形,
是平行四边形, ![]() ,反比例函数
,反比例函数![]() 在第一象限内的图像经过点
在第一象限内的图像经过点![]() ,与
,与![]() 交于点
交于点![]() ,若点
,若点![]() 为
为![]() 的中点,且
的中点,且![]() 的面积为12,则
的面积为12,则![]() 的值为( )
的值为( )
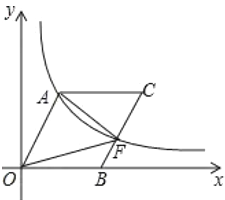
A.16B.24C.36D.48
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中, ![]() ,边
,边![]() 的长为
的长为![]() 边
边![]() 的长为
的长为![]() ,在此三角形内有一个矩形
,在此三角形内有一个矩形![]() ;点
;点![]() 分别在
分别在![]() 上,设
上,设![]() 的长为
的长为![]() ,矩形
,矩形![]() 的面积为
的面积为![]() (单位:
(单位: ![]() )
)
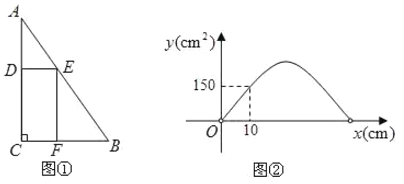
(1)当![]() 等于30时,求
等于30时,求![]() 与
与![]() 的函数关系式:(不要求写出自变量
的函数关系式:(不要求写出自变量![]() 的取值范围)
的取值范围)
(2)在(1)的条件下,矩形![]() 的面积能否为
的面积能否为![]() ?请说明理由?
?请说明理由?
(3)若![]() 与
与![]() 的函数图象如图2所示,求此时
的函数图象如图2所示,求此时![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市今年 1 月份的销售额为 500 万元,超市预计每个月的销售额会逐月增加.预测 3 月 份的销售额比 2 月份增加 120 万元;
(1)求 2、3 月份平均每月销售额的增长率;
(2)按照这样的增长速度,超市想在第一季度完成 1800 万元的销售目标是否能实现?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线.如图所示,点A、B、C、D分别是“蛋圆”与坐标轴的交点,已知点D的坐标为(0,-3),AB为半圆的直径,半圆圆心M的坐标为(1,0),半圆半径为2.

(1)请你求出“蛋圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)你能求出经过点C的“蛋圆”切线的解析式吗?试试看;
(3)开动脑筋想一想,相信你能求出经过点D的“蛋圆”切线的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com