
【题目】如图,两块大小不等的等腰直角三角形按图1放置,点![]() 为直角顶点,点
为直角顶点,点![]() 在
在![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角度
角度![]() ,连接
,连接![]() 、
、![]() .
.
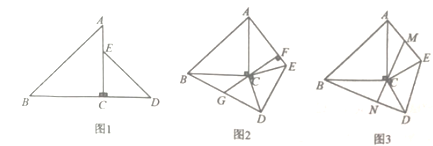
(1)若![]() ,则当
,则当![]()
![]() 时,四边形
时,四边形![]() 是平行四边形;
是平行四边形;
(2)图2,若![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() 是
是![]() 的中点;
的中点;
(3)图3,若点![]() 是
是![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() 时,四边形
时,四边形![]() 是平行四边形;(2)见解析;(3)见解析.
是平行四边形;(2)见解析;(3)见解析.
【解析】
(1)当AC∥DE时,因为AC=DE,推出四边形ACDE是平行四边形,利用平行四边形的性质即可解决问题.
(2)如图2中,作DM⊥FM于M,BN⊥FM交FM的延长线于N.利用全等三角形的性质证明BN=DM,再证明△BNG≌△DMG(AAS)即可解决问题.
(3)如图3中,延长CM到K,使得MK=CM,连接AK.KM.想办法证明△BCD≌△CAK(SAS),即可解决问题.
(1)解:如图1-1中,连接AE.
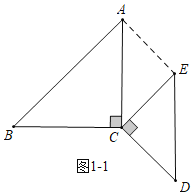
当AC∥DE时,∵AC=DE,
∴四边形ACDE是平行四边形,
∴∠ACE=∠CED,
∵CE=CD,∠ECD=90°,
∴∠CED=45°,
∴α=∠ACE=45°.
故答案为45.
(2)证明:如图2中,作DM⊥FM于M,BN⊥FM交FM的延长线于N.
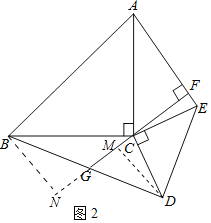
∵CF⊥AE,DM⊥FM,
∴∠CFE=∠CMD=∠ECD=90°,
∴∠ECF+∠CEF=90°,∠ECF+∠DCM=90°,
∴∠CEF=∠DCM,∵CE=CD,
∴△CFE≌△DMC(AAS),
∴DM=CF,
同法可证:CF=BN,
∴BN=DM,
∵BN⊥FM,
∴∠N=∠DMG=90°,
∵∠BGN=∠DGM,
∴△BNG≌△DMG(AAS),
∴BG=DG,
∴点G是BD的中点.
(3)证明:如图3中,延长CM到K,使得MK=CM,连接AK.KM.
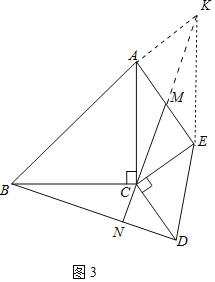
∵AM-ME,CM=MK,
∴四边形ACEK是平行四边形,
∴AK=CE=CD,AK∥CE,
∴∠KAC+∠ACE=180°,
∵∠ACE+∠BCD=180°,
∴∠BCD=∠KAC,
∵CA=CB,CD=AK,
∴△BCD≌△CAK(SAS),
∵∠ACK=∠CBD,
∵∠ACK+∠BCN=90°,
∴∠CBD+∠BCN=90°,
∴∠CNB=90°,
∴CN⊥BD.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°.
(1)求作:∠A的平分线AD,AD交BC于点D;(保留作图痕迹,不写作法)
(2)若点D恰好在线段AB的垂直平分线上,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
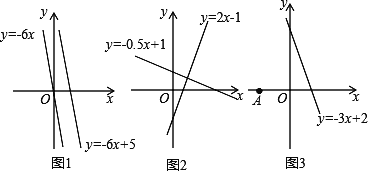
【题目】材料一:如图1,由课本91页例2画函数y=﹣6x与y=﹣6x+5可知,直线y=﹣6x+5可以由直线y=﹣6x向上平移5个单位长度得到由此我们得到正确的结论一:在直线L1:y=K1x+b1与直线L2:y=K2x+b2中,如果K1=K2 且b1≠b2 ,那么L1∥L2,反过来,也成立.
材料二:如图2,由课本92页例3画函数y=2x﹣1与y=﹣0.5x+1可知,利用所学知识一定能证出这两条直线是互相垂直的.由此我们得到正确的结论二:在直线L1:y=k1x+b1 与L2:y=k2x+b2 中,如果k1·k2=-1那么L1⊥L2,反过来,也成立
应用举例
已知直线y=﹣![]() x+5与直线y=kx+2互相垂直,则﹣
x+5与直线y=kx+2互相垂直,则﹣![]() k=﹣1.所以k=6
k=﹣1.所以k=6
解决问题
(1)请写出一条直线解析式______,使它与直线y=x﹣3平行.
(2)如图3,点A坐标为(﹣1,0),点P是直线y=﹣3x+2上一动点,当点P运动到何位置时,线段PA的长度最小?并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
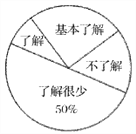
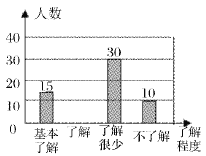
【题目】“食品安全”受到全社会的广泛关注,我市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有_________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________度;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
扇形统计图 条形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的路程(记向东为正)记录如下(x>6且x<14,单位km)

(1)这辆出租车第三次行驶完后在离出发点的 方向;经过连续4次行驶后,这辆车所在的位置 (结果用表示);
(2)这辆出租车一共行驶了多少路程(结果用表示);当x=8时,出租车行驶的路程是多少 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙二人沿着边长为90 m的正方形行走,按A→B→C→D→A…方向,甲从点A出发以70 m/min的速度行走,乙从点B出发以82 m/min的速度行走,当乙第一次追上甲时,在正方形的哪一条边上?
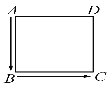
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一张长方形纸片,![]() (
(![]() ).将这张纸片沿着过点
).将这张纸片沿着过点![]() 的折痕翻折,使点
的折痕翻折,使点![]() 落在
落在![]() 边上的点
边上的点![]() ,折痕交
,折痕交![]() 于点
于点![]() ,将折叠后的纸片再次沿着另一条过点
,将折叠后的纸片再次沿着另一条过点![]() 的折痕翻折,点
的折痕翻折,点![]() 恰好与点
恰好与点![]() 重合,此时折痕交
重合,此时折痕交![]() 于点
于点![]() .
.
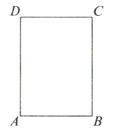
(1)在图中确定点![]() 、点
、点![]() 和点
和点![]() 的位置;
的位置;
(2)联结![]() ,则
,则![]() ______
______![]() ;
;
(3)用含有![]() 的代数式表示线段
的代数式表示线段![]() 的长.(注:直角三角形中,两直角边的平方的和等于斜边的平方)
的长.(注:直角三角形中,两直角边的平方的和等于斜边的平方)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知n边形的内角和θ=(n﹣2)×180°.
(1)甲同学说,θ能取900°;而乙同学说,θ也能取800°.甲、乙的说法对吗?若对,求出边数n.若不对,说明理由;
(2)若n边形变为(n+x)边形,发现内角和增加了540°,用列方程的方法确定x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成任务:
自相似图形
定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
任务:
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为 ;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.已知△ACD∽△ABC,则△ACD与△ABC的相似比为 ;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
请从下列A、B两题中任选一条作答:我选择 题.
A:①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a= (用含b的式子表示);
②如图3﹣2若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a= (用含n,b的式子表示);
B:①如图4﹣1,若将矩形ABCD先纵向分割出2个全等矩形,再将剩余的部分横向分割成3个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含b的式子表示);
②如图4﹣2,若将矩形ABCD先纵向分割出m个全等矩形,再将剩余的部分横向分割成n个全等矩形,且分割得到的矩形与原矩形都相似,则a= (用含m,n,b的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com