
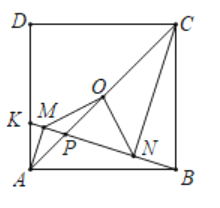
【题目】如图,边长为1的正方形ABCD中,点K在AD上,连接BK,过点A,C作BK的垂线,垂足分别为M,N,点O是正方形ABCD的中心,连接OM,ON.
(1)求证:AM=BN;
(2)请判断△OMN的形状,并说明理由;
(3)若点K在线段AD上运动(不包括端点),设AK=x,△OMN的面积为y,求y关于x的函数关系式(写出x的范围);若点K在射线AD上运动,且△OMN的面积为![]() ,请直接写出AK长.
,请直接写出AK长.
【答案】(1)详见解析;(2)![]() 是等腰直角三角形,理由详见解析;(3)
是等腰直角三角形,理由详见解析;(3)![]() ,
,![]() 长为
长为![]() 或3.
或3.
【解析】
(1)由“AAS”可证△ABM≌△BCN,可得AM=BN;
(2)连接OB,由“SAS”可证△AOM≌△BON,可得MO=NO,∠AOM=∠BON,由余角的性质可得∠MON=90°,可得结论;
(3)由勾股定理可求BK的值,由![]() ,四边形ABCD是正方形,可得:
,四边形ABCD是正方形,可得:![]() ,
,![]() ,则可求得
,则可求得![]() ,由三角形面积公式可求得
,由三角形面积公式可求得![]() ;点K在射线AD上运动,分两种情况:当点K在线段AD上时和当点K在线段AD的延长线时分别求解即可得到结果.
;点K在射线AD上运动,分两种情况:当点K在线段AD上时和当点K在线段AD的延长线时分别求解即可得到结果.
解:(1)证明:
∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
又![]()
∴![]() ≌
≌![]() (AAS)
(AAS)
∴![]()
(2)![]() 是等腰直角三角形
是等腰直角三角形
理由如下:连接![]() ,
,
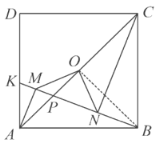
∵![]() 为正方形的中心
为正方形的中心
∴OA=OB,∠OBA=∠OAB=45°=∠OBC,AO⊥BO,
∵∠MAB=∠CBM,
∴![]() ,即
,即![]()
∵![]()
∴![]() ≌
≌![]() (SAS)
(SAS)
∴![]() ,
,![]()
∵![]()
∵∠AON+∠BON=90°,
∴∠AON+∠AOM=90°,
∴![]()
∴![]() 是等腰直角三角形.
是等腰直角三角形.
(3)在![]() 中,
中,![]()
由![]() ,四边形ABCD是正方形,
,四边形ABCD是正方形,
可得:![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,得:
,得:![]()
∴![]() ,得:
,得:![]()
∴![]()
∴![]()
即:![]()
当点K在线段AD上时,则![]() ,
,
解得:x1=3(不合题意舍去),![]() ,
,
当点K在线段AD的延长线时,同理可求得![]()
∴![]() ,
,
解得:x1=3,![]() (不合题意舍去),
(不合题意舍去),
综上所述:![]() 长为
长为![]() 或3时,△OMN的面积为
或3时,△OMN的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是射线
是射线![]() 上一点,
上一点,![]() .动点
.动点![]() 从点
从点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 水平向左作匀速运动,与此同时,动点
水平向左作匀速运动,与此同时,动点![]() 从点
从点![]() 出发,也以
出发,也以![]() 的速度沿
的速度沿![]() 竖直向上作匀速运动.连接
竖直向上作匀速运动.连接![]() ,交
,交![]() 于点
于点![]() .经过
.经过![]() 、
、![]() 、
、![]() 三点作圆,交
三点作圆,交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .设运动时间为
.设运动时间为![]() ,其中
,其中![]() .
.
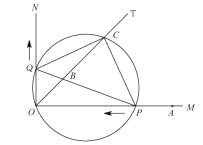
(1)求![]() 的值;
的值;
(2)是否存在实数![]() ,使得线段
,使得线段![]() 的长度最大?若存在,求出
的长度最大?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(3)求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知圆O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
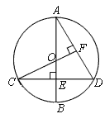
(1)证明:点E是OB的中点;
(2)若AB=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
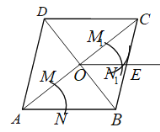
【题目】如图,菱形![]() 的对角线
的对角线![]() 相交于点
相交于点![]() 按下列步骤作图:①以点
按下列步骤作图:①以点![]() 为圆心,任意长为半径作弧,分别交
为圆心,任意长为半径作弧,分别交![]() 于点
于点![]() ;②以点
;②以点![]() 为圆心,
为圆心,![]() 长为半径作弧,交
长为半径作弧,交![]() 于点
于点![]() ;③点
;③点![]() 为圆心,
为圆心,![]() 以长为半径作弧,在
以长为半径作弧,在![]() 内部交②中所作的圆弧于点
内部交②中所作的圆弧于点![]() ;④过点
;④过点![]() 作射线
作射线![]() 交
交![]() 于点
于点![]() .
.![]() ,四边形
,四边形![]() 的面积为( )
的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
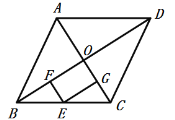
【题目】如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的边
的边![]() 上取一点
上取一点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画⊙O,⊙O与边
为半径画⊙O,⊙O与边![]() 相切于点
相切于点![]() ,
,![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() ,并延长交线段
,并延长交线段![]() 于点
于点![]() .
.
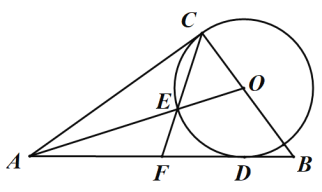
(1)求证:![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若![]() 是
是![]() 的中点,试探究
的中点,试探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
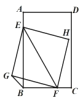
【题目】已知:矩形![]() 的边
的边![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 匀速运动,点
匀速运动,点![]() 同时从点
同时从点![]() 出发沿线段
出发沿线段![]() 向点
向点![]() 匀速运动,速度均为
匀速运动,速度均为![]() ,当一个点到达终点时另一个点也停止运动.连接
,当一个点到达终点时另一个点也停止运动.连接![]() ,以
,以![]() 为对角线作正方形
为对角线作正方形![]() ,连接
,连接![]() ,则
,则![]() 的长度为____.
的长度为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车和慢车分别从![]() 市和
市和![]() 市两地同时出发,匀速行驶,先相向而行,慢车到达
市两地同时出发,匀速行驶,先相向而行,慢车到达![]() 市后停止行驶,快车到达
市后停止行驶,快车到达![]() 市后,立即按原路原速度返回
市后,立即按原路原速度返回![]() 市(调头时间忽略不计),结果与慢车同时到达
市(调头时间忽略不计),结果与慢车同时到达![]() 市.快、慢两车距
市.快、慢两车距![]() 市的路程
市的路程![]() 、
、![]() (单位:
(单位:![]() )与出发时间
)与出发时间![]() (单位:
(单位:![]() )之间的函数图像如图所示.
)之间的函数图像如图所示.
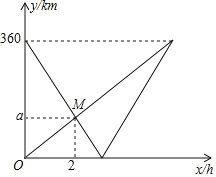
(1)![]() 市和
市和![]() 市之间的路程是________
市之间的路程是________![]() ,图中
,图中![]() ____________;
____________;
(2)请求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)快车与慢车迎面相遇以后,请直接写出经过多长时间两车相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
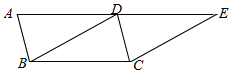
【题目】如图,四边形ABCD是平行四边形,AD=BD,过点C作CE∥BD,交AD的延长线于点E.
(1)求证:四边形BDEC是菱形;
(2)连接BE,若AB=2,AD=4,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com