
 在讲完《平行线的性质》后,老师出了一道题:如图所示,∠1=65°,∠2=∠65°,∠3=60°,求∠4的度数.小刚看了题目后说:“题中给出∠1和∠2的度数是多余的,因为∠3和∠5是一对同位角,而同位角相等,所以∠5=∠3=60°.又根据对顶角相等得∠4=∠5=60°.你认为小刚的说法对吗?并说明原因.
在讲完《平行线的性质》后,老师出了一道题:如图所示,∠1=65°,∠2=∠65°,∠3=60°,求∠4的度数.小刚看了题目后说:“题中给出∠1和∠2的度数是多余的,因为∠3和∠5是一对同位角,而同位角相等,所以∠5=∠3=60°.又根据对顶角相等得∠4=∠5=60°.你认为小刚的说法对吗?并说明原因.  名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过A作AT⊥BE于T点,写出AT+TE与BE之间的数量关系.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,过A作AT⊥BE于T点,写出AT+TE与BE之间的数量关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
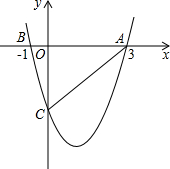 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+$\frac{1}{2}$b)-(-$\frac{1}{3}$c+$\frac{2}{7}$)=a+$\frac{1}{2}$b+$\frac{1}{3}c$-$\frac{2}{7}$ | B. | m+(-n+a-b)=m-n+a-b | ||
| C. | x-(3y-$\frac{1}{2}$)=x-3y+$\frac{1}{2}$ | D. | -$\frac{1}{2}$(4x-6y+3)=-2x+3y+3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com