
【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.过点A作AF⊥AB,并截取AF=BD,连接DC,DF,CF. 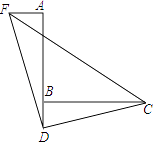
(1)判断△CDF的形状并证明.
(2)若BC=6,AF=2,求AB的长.
【答案】
(1)解:△CDF为等腰直角三角形.理由如下:
∵AF⊥AB,
∴∠DAF=90°,
在△ADF和△BCD中
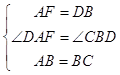 ,
,
∴△ADF≌△BCD,
∴DF=CD,∠ADF=∠BCD,
∵∠BCD+∠CDB=90°,
∴∠ADF+∠CDB=90°,即∠CDF=90°,
∴△CDF为等腰直角三角形
(2)解:∵△ADF≌△BCD,
∴AD=BC=6,AF=BD=2,
∴AB=AD﹣BD=6﹣2=4
【解析】(1)理由“ASA”证明△ADF≌△BCD得到DF=CD,∠ADF=∠BCD,再利用∠BCD+∠CDB=90°得到∠CDF=90°,则可判断△CDF为等腰直角三角形;(2)由△ADF≌△BCD得到AD=BC=6,AF=BD=2,然后计算AD﹣BD即可.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】下面是小林画出函数 ![]() 的一部分图象,利用图象回答:
的一部分图象,利用图象回答: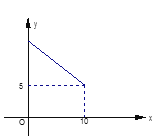
(1)自变量x的取值范围.
(2)当x取什么值时,y的最小值.最大值各是多少?
(3)在图中,当x增大时,y的值是怎样变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于D,交AB于E,∠DBC=15°,则∠A的度数是( ) 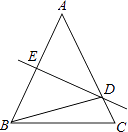
A.50°
B.20°
C.30°
D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( ) 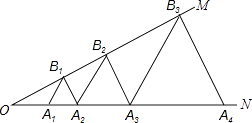
A.6
B.12
C.32
D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线交BC的延长线于点F. 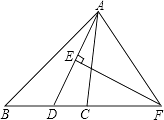
(1)求证:∠FAD=∠FDA;
(2)若∠B=50°,求∠CAF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列各组角的位置,判断错误的是( ) 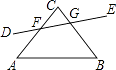
A.∠C和∠CFG是同旁内角
B.∠CGF和∠AFG是内错角
C.∠BGF和∠A是同旁内角
D.∠BGF和∠AFD是同位角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com