
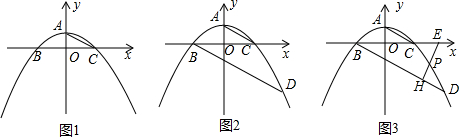
分析 (1)先求出A、C两点坐标,利用待定系数法即可解决问题.
(2)假设直线BD解析式为y=-2ax+b′,把(-2,0)代入得到,b′=-4a,可得直线BD解析式为y=-2ax-4a,设点D坐标为(m,-3),由-3=-2am-4a,可得m=$\frac{3-4a}{2a}$,推出D($\frac{3-4a}{2a}$,-3)代入y=-ax2+4a,解方程即可.
(3)如图3中,作HM⊥BE于M,PJ⊥BE于J,直线BD交y轴于N.设P(m,-$\frac{1}{4}$m2+1),想办法用m的代数式表示PJ、OM、EM、OJ再根据JE=$\frac{1}{2}$PJ=OM+EM-OJ列出方程即可解决问题.
解答 解:(1)如图1中,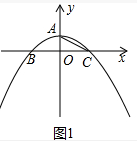
x=0得y=4a,令y=0,得-ax2+4a=0,解得x=±2,
∴A(0,4a),B(-2,0),A(2,0),
设直线AC解析式为y=kx+b,则有$\left\{\begin{array}{l}{b=4a}\\{2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2a}\\{b=4a}\end{array}\right.$,
∴直线AC解析式为y=-2ax+4a.
(2)如图2中,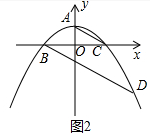
∵BD∥AC,
∴可以假设直线BD解析式为y=-2ax+b′,把(-2,0)代入得到,b′=-4a,
∴直线BD解析式为y=-2ax-4a,
设点D坐标为(m,-3),
∴-3=-2am-4a,
∴m=$\frac{3-4a}{2a}$,
∴D($\frac{3-4a}{2a}$,-3)代入y=-ax2+4a,得-3=-a•($\frac{3-4a}{2a}$)2+4a,
解得a=$\frac{1}{4}$,
∴抛物线解析式为y=-$\frac{1}{4}$x2+1.
(3)如图3中,作HM⊥BE于M,PJ⊥BE于J,直线BD交y轴于N.设P(m,-$\frac{1}{4}$m2+1),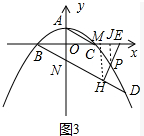
由(2)可知D(4,-3),直线BD解析式为y=-$\frac{1}{2}$x-1,
∴N(0,-1),
∵EH⊥BD,HM⊥BE,
∴∠EHM+∠BHM=90°,∠HBM+∠BHM=90°,
∴∠EHM=∠HBM,
∵PJ∥HM,
∴∠EPJ=∠EHM=∠HBM,
∴tan∠EPJ=tan∠EHM=tan∠HBM=$\frac{1}{2}$,
∵$\frac{JP}{HM}$=$\frac{EP}{EH}$=$\frac{5}{9}$,JP=$\frac{1}{4}$m2-1,
∴HM=$\frac{9}{5}$($\frac{1}{4}$m2-1),BM=$\frac{18}{5}$($\frac{1}{4}$m2-1),
∴OM=$\frac{18}{5}$($\frac{1}{4}$m2-1)-2,EM=$\frac{1}{2}$HM=$\frac{9}{10}$($\frac{1}{4}$m2-1),
∵JE=$\frac{1}{2}$PJ=OM+EM-OJ
∴$\frac{1}{2}$($\frac{1}{4}$m2-1)=$\frac{18}{5}$($\frac{1}{4}$m2-1)-2+$\frac{9}{10}$($\frac{1}{4}$m2-1)-m,
整理得到10m2-19m-51=0,解得m=$\frac{17}{5}$或-$\frac{3}{2}$(舍弃),
∴点P坐标为($\frac{17}{5}$,-$\frac{189}{100}$).
点评 本题考查二次函数综合题、一次函数、锐角三角函数、待定系数法等知识,解题的关键是灵活应用所学知识解决问题,学会利用参数,构造方程解决问题,属于中考压轴题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 由于持续高温和连日无雨,某水库的需水量随着时间的增加而减少,干旱持续时间t(天)与蓄水量v(万立方米)的关系如图所示.请你根据图象所提供的信息回答下列问题.
由于持续高温和连日无雨,某水库的需水量随着时间的增加而减少,干旱持续时间t(天)与蓄水量v(万立方米)的关系如图所示.请你根据图象所提供的信息回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
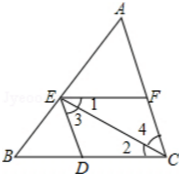
| A. | ∠1=∠3 | B. | ∠3=∠A | C. | ∠1=∠2 | D. | ∠1=∠A |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,3) | B. | (-1,-3) | C. | (-1,3) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:
如图,四边形ABCD为⊙O的内接四边形,对边BC,AD交于点F,AB、DC交于点E,△ECF的外接圆与⊙O的另一交点为H,AH与EF交于点M,MC与⊙O交于点C.证明:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
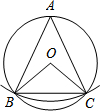 如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )
如图,AB是⊙O的弦(AB不是直径),以点A为圆心,以AB长为半径画弧交⊙O于点C,连结AC、BC、OB、OC.若∠ABC=65°,则∠BOC的度数是( )| A. | 50° | B. | 65° | C. | 100° | D. | 130° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别与EF,GF交于I,H两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将抛物线在第四象限之间的部分图象记为图象G,如果直线y=k(x+1)-4与图象G有公共点,请结合图象,求直线y=k(x+1)-4与y轴交点的纵坐标t的取值范围.
将抛物线在第四象限之间的部分图象记为图象G,如果直线y=k(x+1)-4与图象G有公共点,请结合图象,求直线y=k(x+1)-4与y轴交点的纵坐标t的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
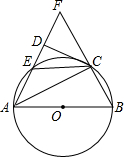 如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,
如图,在△ABF中,以AB为直径的圆分别交边AF、BF于C、E两点,CD⊥AF.AC是∠DAB的平分线,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com