
分析 (1)将(0,2)代入抛物线解析式求得a的值,从而得出抛物线的解析式,再令y=0,得出x的值,即可求得点A、B的坐标;
(2)如图2,作A'H⊥x轴于H,可证明△AOC∽△COB,得出∠ACO=∠CBO,由A'H∥OC,即可得出A′H的长,即可求得A′的坐标;
(3)分两种情况:①如图3,以AB为直径作⊙M,⊙M交抛物线的对称轴于P(BC的下方),由圆周角定理得出点P坐标;②如图4,类比第(2)小题的背景将△ABC沿直线BC对折,点A的对称点为A',以A'B为直径作⊙M',⊙M'交抛物线的对称轴于P'(BC的上方),作M'E⊥A'H于E,交对称轴于F,求得M'F,在Rt△M'P'F中,由勾股定理得出P'F得的长,从而得出点P的坐标即可.
解答 解:(1)把C(0,2)代入y=ax2-3ax-4a得-4a=2,
解得$a=-\frac{1}{2}$.
所以抛物线的解析式为$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2$.
令$-\frac{1}{2}{x^2}+\frac{3}{2}x+2=0$,可得:x1=-1,x2=4.
所以A(-1,0),B(4,0).
(2)如图2,作A'H⊥x轴于H,
因为$\frac{OA}{OC}=\frac{OC}{OB}=\frac{1}{2}$,且∠AOC=∠COB=90°,
所以△AOC∽△COB,
所以∠ACO=∠CBO,可得∠ACB=∠OBC+∠BCO=90°,
由A'H∥OC,AC=A'C得OH=OA=1,A'H=2OC=4;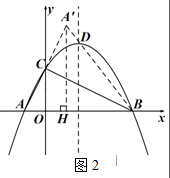
所以A'(1,4);
(3)分两种情况:
①如图3,以AB为直径作⊙M,⊙M交抛物线的对称轴于P(BC的下方),
由圆周角定理得∠CPB=∠CAB,
易得:MP=$\frac{1}{2}$AB.所以P($\frac{3}{2}$,$-\frac{5}{2}$).
②如图4,类比第(2)小题的背景将△ABC沿直线BC对折,
点A的对称点为A',以A'B为直径作⊙M',⊙M'交抛物线的对称轴于P'(BC的上方),
则∠CP2B=∠CA'B=∠CAB.
作M'E⊥A'H于E,交对称轴于F.
则M'E=$\frac{1}{2}$BH=$\frac{3}{2}$,EF=$\frac{3}{2}-1$=$\frac{1}{2}$.
所以M'F=$\frac{3}{2}-\frac{1}{2}$=1.
在Rt△M'P'F中,P'F=$\sqrt{(\frac{5}{2}{)^2}-{1^2}}=\frac{{\sqrt{21}}}{2}$,
所以P'M=2+$\frac{{\sqrt{21}}}{2}$.
所以P'($\frac{3}{2}$,2+$\frac{{\sqrt{21}}}{2}$).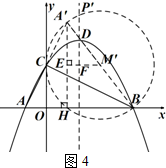
综上所述,P的坐标为($\frac{3}{2}$,$-\frac{5}{2}$)或($\frac{3}{2}$,2+$\frac{{\sqrt{21}}}{2}$).
点评 本题考查了二次函数的相关性质、一次函数的相关性质、一元二次方程的解法以及二次根式的运算、勾股定理等.本题解题技巧要求高,而且运算复杂,因此对考生的综合能力提出了很高的要求.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
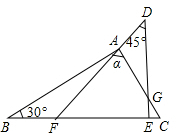 小雪是个爱动脑的同学,有一天她把手中的一副三角板拼在一起,如图所示,这样除了三角板原有的6个角外,又出现了几个角,如图图中的α,她想,能不能借助三角板中已知角的度数,把这些角分别求出来呢?经过一番思考,她发现图中其他8个角(包括∠α)的度数是可以求出来的!聪明的同学,请你把这些角找出来,然后一一求出它们的度数,相信你能行!
小雪是个爱动脑的同学,有一天她把手中的一副三角板拼在一起,如图所示,这样除了三角板原有的6个角外,又出现了几个角,如图图中的α,她想,能不能借助三角板中已知角的度数,把这些角分别求出来呢?经过一番思考,她发现图中其他8个角(包括∠α)的度数是可以求出来的!聪明的同学,请你把这些角找出来,然后一一求出它们的度数,相信你能行!查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com