
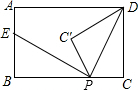
 如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:
如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:分析 连接DE,根据折叠的性质可得∠CPD=∠C′PD,再根据角平分线的定义可得∠BPE=∠C′PE,然后证明∠DPE=90°,从而得到△DPE是直角三角形,再分别表示出AE、CP的长度,然后利用勾股定理进行列式整理即可得到y与x的函数关系式,即可得解.
解答 解:如图,连接DE,∵△PC′D是△PCD沿PD折叠得到,
∴∠C′=∠C=90°,∠CPD=∠C′PD,
∴∠CDC′+∠CPC′=∠CPC′+∠BPC′=180°,
∠BPC′=∠CDC';故①正确;
∵PE平分∠BPC′,
∴∠BPE=∠C′PE,
∴∠EPC′+∠DPC′=$\frac{1}{2}$×180°=90°,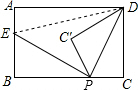
∴△DPE是直角三角形,
∵BP=x,BE=y,AB=3,BC=5,
∴AE=AB-BE=3-y,CP=BC-BP=5-x,
在Rt△BEP中,PE2=BP2+BE2=x2+y2,
在Rt△ADE中,DE2=AE2+AD2=(3-y)2+52,
在Rt△PCD中,PD2=PC2+CD2=(5-x)2+32,
在Rt△PDE中,DE2=PE2+PD2,
则(3-y)2+52=x2+y2+(5-x)2+32,
整理得,-6y=2x2-10x,
所以y=-$\frac{1}{3}$x2+$\frac{5}{3}$x(0<x<5),故②正确;
∵∠BPE=∠C′PE,∠CPD=∠C′PD,
∴∠BPE+∠CPD=90°,
∵点P为BC的中点,
∴CP=$\frac{5}{2}$,∵CD=AB=3,
∴CP≠CD,
∴∠CPD≠45°,
∴∠BPE≠45°,
∴△BPE不是等腰直角三角形,故③错误;
∵y=-$\frac{1}{3}$x2+$\frac{5}{3}$x=-$\frac{1}{3}$(x-$\frac{5}{2}$)2+$\frac{25}{12}$,
∴x=$\frac{5}{2}$时.y取最大值,
∴PB=$\frac{5}{2}$,
∴PC=$\frac{5}{2}$,
∴△DCP的面积=$\frac{1}{2}×$$\frac{5}{2}$×4=5,矩形ABCD面积=4×5=20,
∴△DCP的面积是矩形ABCD面积的$\frac{1}{4}$.故④正确;
故答案为:①②④.
点评 本题考查了翻折变换-折叠问题,勾股定理的应用,作出辅助线并证明得到直角三角形,熟练正确折叠的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
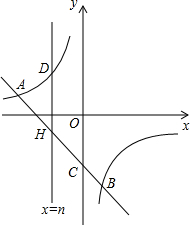 如图,已知直线l:y=ax+b与反比例函数y=-$\frac{4}{x}$的图象交于A(-4,1)、B(m,-4),且直线l与y轴交于点C.
如图,已知直线l:y=ax+b与反比例函数y=-$\frac{4}{x}$的图象交于A(-4,1)、B(m,-4),且直线l与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为4cm.
如图,?ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为4cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
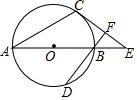 如图,AB是⊙O的直径,AC是⊙O的弦,E是AB延长线上的点,BF⊥EC于F交⊙O于D,∠EBF=2∠EAC.
如图,AB是⊙O的直径,AC是⊙O的弦,E是AB延长线上的点,BF⊥EC于F交⊙O于D,∠EBF=2∠EAC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com