
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是角平分线,
是角平分线,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,经过
,经过![]() 两点的
两点的![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 恰为
恰为![]() 的直径.
的直径.
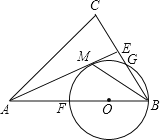
(1)求证:![]() 与
与![]() 相切;
相切;
(2)当![]() 时,求
时,求![]() 的半径.
的半径.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OM,证明OM∥BE,再结合等腰三角形的性质说明AE⊥BE,进而证明OM⊥AE;
(2)结合已知求出AB,再证明△AOM∽△ABE,利用相似三角形的性质计算.
(1)连接OM,则OM=OB,
∴∠1=∠2,
∵BM平分∠ABC,
∴∠1=∠3,
∴∠2=∠3,
∴OM∥BC,
∴∠AMO=∠AEB,
在△ABC中,AB=AC,AE是角平分线,
∴AE⊥BC,
∴∠AEB=90°,
∴∠AMO=90°,
∴OM⊥AE,
∵点M在圆O上,
∴AE与⊙O相切;
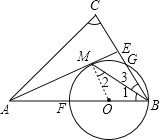
(2)在△ABC中,AB=AC,AE是角平分线,
∴BE=![]() BC,∠ABC=∠C,
BC,∠ABC=∠C,
∵BC=4,cosC=![]()
∴BE=2,cos∠ABC=![]() ,
,
在△ABE中,∠AEB=90°,
∴AB=![]() =6,
=6,
设⊙O的半径为r,则AO=6-r,
∵OM∥BC,
∴△AOM∽△ABE,
∴∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() 的半径为
的半径为![]() .
.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】为迎接国庆节,某商店购进了一批成本为每件30元的纪念商品.经调查发现,该商品每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
(元![]() 满足一次函数关系,其图象如图所示.
满足一次函数关系,其图象如图所示.

(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)若商店按不低于成本价,且不高于60元的单价销售,则销售单价定为多少,才能使销售该商品每天获得的利润![]() (元
(元![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区的居民用电,按照高峰时段和空闲时段规定了不同的单价.某户5月份高峰时段用电量是空闲时段用电量2倍,6月份高峰时段用电量比5月份高峰时段用电量少50%,结果6月份的用电量和5月份的用电量相等,但6月份的电费却比5月份的电费少25%,求该地区空闲时段民用电的单价比高峰时段的用电单价低的百分率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
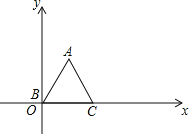
【题目】已知等边△ABC,顶点B(0,0),C(2,0),规定把△ABC先沿x轴绕着点C顺时针旋转,使点A落在x轴上,称为一次变换,再沿x轴绕着点A顺时针旋转,使点B落在x轴上,称为二次变换,…经过连续2018次变换后,顶点A的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。

(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.

(1)确定k的值: ;
(2)计算△OAB的面积;
(3)若点D(3,b)在双曲线y=![]() (x>0)上,直线AD的解析式为y=mx+n,请直接写出不等式mx+n<
(x>0)上,直线AD的解析式为y=mx+n,请直接写出不等式mx+n<![]() 的解集: .
的解集: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,DC为⊙O的切线,DE⊥AB,垂足为点E,交⊙O于点F,弦AC交DE于点P,连接CF.
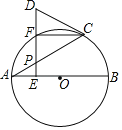
(1)求证:∠DPC=∠PCD;
(2)若AP=2,填空:
①当∠CAB= 时,四边形OBCF是菱形;
②当AC=2AE时,OB= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 为
为![]() 边上一动点(点
边上一动点(点![]() 与点
与点![]() 不重合),联结
不重合),联结![]() ,过点
,过点![]() 作
作![]() 交边
交边![]() 于点
于点![]() .
.
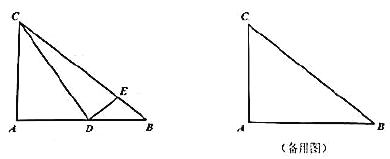
(1)如图,当![]() 时,求
时,求![]() 的长;
的长;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数解析式并写出函数定义域;
的函数解析式并写出函数定义域;
(3)把![]() 沿直线
沿直线![]() 翻折得
翻折得![]() ,联结
,联结![]() ,当
,当![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]()
(1)如图1,若![]() ,
,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 与
与![]() 垂直,求证:
垂直,求证:![]()
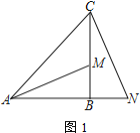
(2)过点![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
①如图2,若![]() ,求证:
,求证:![]()
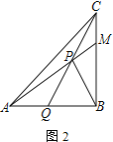
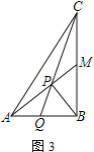
②如图3,若![]() 是
是![]() 的中点,直接写出
的中点,直接写出![]() 的值(用含
的值(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com