
 如图,使用圆规和直尺分别画出∠AOB和∠BOC的角平分线OM和ON,如果∠MON=68°,那么:
如图,使用圆规和直尺分别画出∠AOB和∠BOC的角平分线OM和ON,如果∠MON=68°,那么:科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
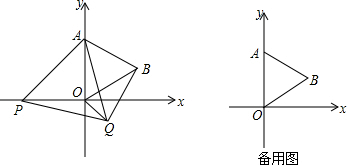
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
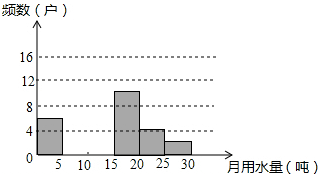 八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:
八年级某班同学为了了解2012年某居委会家庭月均用水情况,随机调查了该居委会部分家庭,并将调查数据进行如下调整:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | a | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | 0.08 |
| 25<x≤30 | 2 | 0.04 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
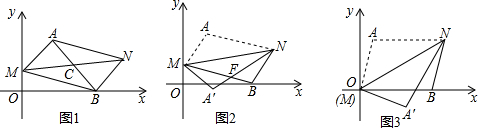
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com