
 如图,在梯形ABCD中,AD∥BC,AD=3,BC=9,AB=6,CD=4.若EF∥BC,且梯形AEFD与梯形EBCF的周长相等,则EF的长为$\frac{39}{5}$.
如图,在梯形ABCD中,AD∥BC,AD=3,BC=9,AB=6,CD=4.若EF∥BC,且梯形AEFD与梯形EBCF的周长相等,则EF的长为$\frac{39}{5}$. 分析 根据两梯形的周长相等可得AD+AE+EF+FD=EF+EB+BC+CF继而可得:AD+AE+FD=EB+BC+CF=$\frac{1}{2}$,设$\frac{AE}{EB}$=$\frac{DF}{FC}$=k,AE,DF都可用k表示出来,从而可得出k的值,再运用平行的性质即可解出EF的长.
解答 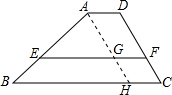 解:由已知AD+AE+EF+FD=EF+EB+BC+CF,
解:由已知AD+AE+EF+FD=EF+EB+BC+CF,
∴AD+AE+FD=EB+BC+CF=$\frac{1}{2}$(AD+AB+BC+CD)=11,
∵EF∥BC,
∴EF∥AD,
∴$\frac{AE}{EB}$=$\frac{DF}{FC}$,
设$\frac{AE}{EB}$=$\frac{DF}{FC}$=k,
∴AE=$\frac{k}{k+1}$AB=$\frac{6k}{k+1}$,DF=$\frac{k}{k+1}$CD=$\frac{4k}{k+1}$,
∴AD+AE+FD=3+$\frac{6k}{k+1}$+$\frac{4k}{k+1}$=$\frac{13k+3}{k+1}$,
∴$\frac{13k+3}{k+1}$=11,
解得:k=4,
作AH∥CD,交BC于H,交EF于G,
则GF=HC=AD=3,BH=BC-CH=9-3=6,
∵$\frac{EG}{BH}=\frac{AE}{AB}=\frac{4}{5}$,
∴EG=$\frac{4}{5}$BH=$\frac{24}{5}$,
∴EF=EG+GF=$\frac{24}{5}$+3=$\frac{39}{5}$.
故答案为:$\frac{39}{5}$.
点评 本题考查了平行线分线段成比例的知识,梯形的性质,正确的作出辅助线是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 根据所给图形(如图)填空.
根据所给图形(如图)填空.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
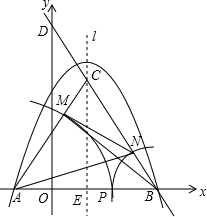 如图所示,抛物线y=-x2+2x+8与x轴交于A、B两点,直线BD的解析式为y=-2$\sqrt{3}x$+8$\sqrt{3}$,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.
如图所示,抛物线y=-x2+2x+8与x轴交于A、B两点,直线BD的解析式为y=-2$\sqrt{3}x$+8$\sqrt{3}$,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
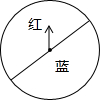 如图是一个红,蓝两色各占一半的转盘,小李与小明做“配紫色”的游戏.规则是:两人各让转盘自由转动一次.当转盘停止转动时.如果指针所在区域的颜色配成紫色.小明胜:如果指针所在区域的颜色配不成紫色.小李胜.在这个游戏中.小李与小明获胜的概率分别是多少?该游戏规则对双方公平吗?为什么?
如图是一个红,蓝两色各占一半的转盘,小李与小明做“配紫色”的游戏.规则是:两人各让转盘自由转动一次.当转盘停止转动时.如果指针所在区域的颜色配成紫色.小明胜:如果指针所在区域的颜色配不成紫色.小李胜.在这个游戏中.小李与小明获胜的概率分别是多少?该游戏规则对双方公平吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com