
【题目】在![]() 中,
中,![]() ,点
,点![]() 为直线
为直线![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),分别作
不重合),分别作![]() 和
和![]() 的角平分线,两角平分线所在直线交于点
的角平分线,两角平分线所在直线交于点![]() .
.
(1)若点![]() 在线段
在线段![]() 上,如图1.
上,如图1.
①依题意补全图1;
②求![]() 的度数;
的度数;
(2)当点![]() 在直线
在直线![]() 上运动时,
上运动时,![]() 的度数是否变化?若不变,请说明理由;若变化,画出相应的图形,并直接写出
的度数是否变化?若不变,请说明理由;若变化,画出相应的图形,并直接写出![]() 的度数.
的度数.



【答案】(1)①补图见解析;②45°;(2)图见解析,∠BEC的度数为45°或135°.
【解析】
(1)①根据题意作图即可;②设∠EBO=∠EBC=![]() ,∠BCK=∠ACK=
,∠BCK=∠ACK=![]() ,由三角形外角定理列方程组求
,由三角形外角定理列方程组求![]() 的度数;
的度数;
(2)分情况讨论点C在OA和AO延长线上时![]() 的度数,结合(1),即点C在线段OA上时
的度数,结合(1),即点C在线段OA上时![]() 的度数,可得结论.
的度数,可得结论.
(1)①依题意补图如下:

②设∠EBO=∠EBC=![]() ,∠BCK=∠ACK=
,∠BCK=∠ACK=![]() ,
,
∵∠ACB=∠OBC+∠BOC,∠BCK=∠EBC+∠BEC
∴![]()
∴∠BEC=45°
(2)如图,当点C在OA延长线上时,
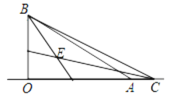
∵∠AOB=90°,
∴∠OBC+∠OCB=90°,
∵BE、CE分别是![]() 和
和![]() 的角平分线,
的角平分线,
∴∠EBC+∠ECB=90°×![]() =45°,
=45°,
∴∠BEC=180°-45°=135°;
如图,当点C在AO延长线上时,
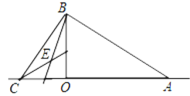
同理,可得∠BEC=135°;
由(1)知,当点C在线段OA上时,∠BEC=135°.
综上可知,当点![]() 在直线
在直线![]() 上运动时,
上运动时,![]() 的度数为45°或135°.
的度数为45°或135°.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:
【题目】完成下面的证明:已知如图,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,且
,且![]() .
.

求证:![]() .
.
证明:![]() 平分
平分![]() (__________)
(__________)
![]() (__________)
(__________)
![]() 平分
平分![]() (已知)
(已知)
![]() ____________(角的平分线的定义).
____________(角的平分线的定义).
![]() ___________
___________ ![]() ___________
___________![]() (____________)
(____________)
![]() (___________),
(___________),
![]() ____________(___________)
____________(___________)
![]() (___________).
(___________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个含有多个字母的式子中,如果任意交换两个字母的位置,式子的值都不变,这样的式子就叫做对称式.例如: ![]() ,
, ![]() ,
, ![]() ,
, ![]()
含有两个字母![]() ,
, ![]() 的对称式的基本对称式是
的对称式的基本对称式是![]() 和
和![]() ,像
,像![]() ,
, ![]() 等对称式都可以用
等对称式都可以用![]() 和
和![]() 表示,例如:
表示,例如: ![]() .
.
请根据以上材料解决下列问题:
(![]() )式子①
)式子①![]() ,②
,②![]() ,③
,③![]() 中,属于对称式的是__________(填序号).
中,属于对称式的是__________(填序号).
(![]() )已知
)已知![]() .
.
①若![]() ,
, ![]() ,求对称式
,求对称式![]() 的值.
的值.
②若![]() ,直接写出对称式
,直接写出对称式![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于P,Q两点给出如下定义:若点P到x,y轴的距离中的最大值等于点Q到x,y轴的距离中的最大值,则称P,Q两点为“等距点”图中的P,Q两点即为“等距点”.

(1)已知点A的坐标为![]() .①在点
.①在点![]()
![]()
![]() 中,为点A的“等距点”的是________;②若点B的坐标为
中,为点A的“等距点”的是________;②若点B的坐标为![]() ,且A,B两点为“等距点”,则点B的坐标为________.
,且A,B两点为“等距点”,则点B的坐标为________.
(2)若![]()
![]() 两点为“等距点”,求k的值.
两点为“等距点”,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

![]() 请用两种不同的方法求图2中阴影部分的面积
请用两种不同的方法求图2中阴影部分的面积![]() 直接用含m,n的代数式表示
直接用含m,n的代数式表示![]()
方法1:______
方法2:______
![]() 根据
根据![]() 中结论,请你写出下列三个代数式之间的一个等量关系: ______;代数式:
中结论,请你写出下列三个代数式之间的一个等量关系: ______;代数式:![]() ,
,![]() ,mn
,mn
![]() 根据
根据![]() 题中的等量关系,解决如下问题:已知
题中的等量关系,解决如下问题:已知![]() ,
,![]() ,求
,求![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知CB//OA,∠C=∠A=104°,点E,F在BC上,OE平分∠COF,OB平分∠AOF
(1)求证:OC//AB;
(2)求∠EOB的度数;
(3)若平行移动AB,在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,BD平分∠CBA交AC于点D,DE⊥AB于点E,且△DEA的周长为2019cm,则AB=______.
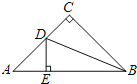
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com