
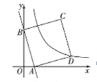
【题目】如图,在平面直角坐标系中,一次函数y=-4x+4的图像与x轴,y轴分别交于A,B两点,正方形ABCD的顶点C,D在第一象限,顶点D在反比例函数![]() 的图像上,若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图像上,则n的值是( )
的图像上,若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图像上,则n的值是( )
A.2B.3C.4D.5
【答案】B
【解析】
由一次函数的关系式可以求出与x轴和y轴的交点坐标,即求出OA,OB的长,由正方形的性质,三角形全等可以求出DE、AE、CF、BF的长,进而求出G点的坐标,最后求出CG的长就是n的值.
如图过点D、C分别做DE⊥x轴,CF⊥y轴,垂足分别为E,F.

CF交反比例函数的图像于点G.
把x=0和y=0分别代入y=-4x+4
得y=4和x=1
∴A(1,0),B(0,4)
∴OA=1,OB=4
由ABCD是正方形,易证
△AOB≌△DEA≌△BCF(AAS)
∴DE=BF=OA=1,AE=CF=OB=4
∴D(5,1),F(0,5)
把D点坐标代入反比例函数y=![]() ,得k=5
,得k=5
把y=5代入y=![]() ,得x=1,即FG=1
,得x=1,即FG=1
CG=CF-FG=4-1=3,即n=3
故答案为B.


科目:初中数学 来源: 题型:
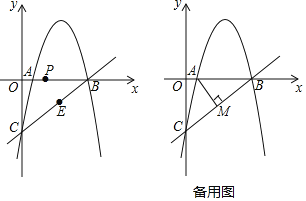
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
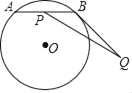
【题目】如图,⊙O上有一个动点A和一个定点B,令线段AB的中点是点P,过点B作⊙O的切线BQ,且BQ=3,现测得![]() 的长度是
的长度是![]() ,
,![]() 的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
的度数是120°,若线段PQ的最大值是m,最小值是n,则mn的值是( )
A. 3![]() B. 2
B. 2![]() C. 9 D. 10
C. 9 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
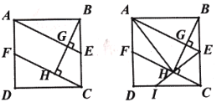
【题目】如图1,正方形ABCD中,点E是BC的中点,过点B作BG⊥AE于点G,过点C作CF垂直BG的延长线于点H,交AD于点F
(1)求证:△ABG≌△BCH;
(2)如图2,连接AH,连接EH并延长交CD于点I;
求证:① AB2=AE·BH;② 求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮将笔记本电脑水平放置在桌子上,显示屏OA与底板OB所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架BCO'后,电脑转到B O′A′位置(如图3),侧面示意图为图4.已知OA=OB=28cm,O′C⊥OB于点C,O′C=14cm.
(参考数据:![]() ,
,![]() ,
,![]() )
)
(1)求∠CBO'的度数.
(2)显示屏的顶部A'比原来升高了多少cm?(结果精确到0.1cm)
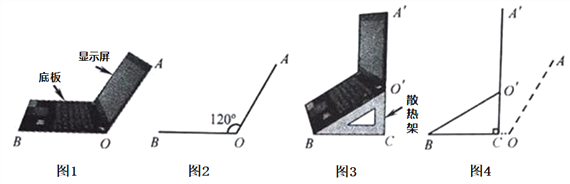
(3)如图4,垫入散热架后,要使显示屏O′A′与水平线的夹角仍保持120°,则显示屏O′A′应绕点O'按顺时针方向旋转多少度?(不写过程,只写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 为对角线
为对角线![]() 上任意一点(不与
上任意一点(不与![]() 重合)连接
重合)连接![]() ,过点M作
,过点M作![]() 交
交![]() (或
(或![]() 的延长线)于点
的延长线)于点![]() ,连接
,连接![]() .
.
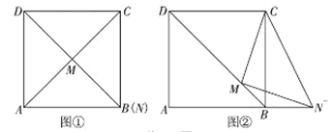
感知:如图①,当M为![]() 中点时,容易证
中点时,容易证![]() (不用证明);
(不用证明);
探究:如图②,点M为对角线![]() 上任意一点(不与
上任意一点(不与![]() 重合)请探究
重合)请探究![]() 与
与![]() 的数量关系,并证明你的结论.
的数量关系,并证明你的结论.
应用:(1)直接写出![]() 的面积S的取值范围;
的面积S的取值范围;
(2)若![]() ,则
,则![]() 与
与![]() 的数量关系是_____________.
的数量关系是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
等级 | 频数 | 频率 |
优秀 | 20 |
|
良好 | ||
合格 | 10 |
|
不合格 | 5 |
|
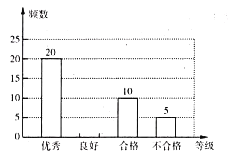
请根据以上信息,解答下列问题:
(1)本次调查随机抽取了______名学生;表中![]() ______,
______,![]() ______;
______;
(2)补全条形统计图;
(3)若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与证明:如图1,把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AF.取AF中点M,EF的中点N,连接MD、MN.
(1)连接AE,求证:△AEF是等腰三角形;
猜想与发现:
(2)在(1)的条件下,请判断MD、MN的数量关系和位置关系,得出结论.
结论1:DM、MN的数量关系是 ;
结论2:DM、MN的位置关系是 ;
拓展与探究:
(3)如图2,将图1中的直角三角板ECF绕点C顺时针旋转180°,其他条件不变,则(2)中的两个结论还成立吗?若成立,请加以证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个菱形①②③④的较小内角均与已知平行四边形ABCD的∠A相等,边长各不相同.将这四个菱形如图所示放入平行四边形中,未被四个菱形覆盖的部分用阴影表示.若已知两个阴影部分的周长的差,则不需测量就能知道周长的菱形为( )
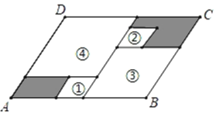
A.①B.②C.③D.④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com