
【题目】如图,平面直角坐标系中,![]()
![]() 轴,点
轴,点![]() 从原点
从原点![]() 出发在
出发在![]() 轴上以
轴上以![]() 单位/秒的速度向
单位/秒的速度向![]() 轴的正方向运动,运动的时间为
轴的正方向运动,运动的时间为![]() 秒.
秒.![]() 平分
平分![]() . (提示:
. (提示:![]() 中,
中,![]() ,若
,若![]() 则
则![]() ,反之亦然)
,反之亦然)
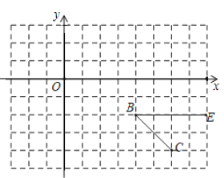
(1)当![]() 时,
时,![]() ;
;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 点运动的时间
点运动的时间![]() ;
;
(3)当![]() 时,求
时,求![]() 的度数(用含
的度数(用含![]() 的式子表示,且不含绝对值).
的式子表示,且不含绝对值).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)求出点A的坐标即可判断.
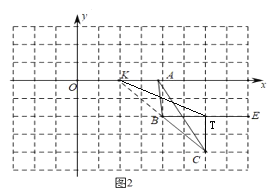
(2)如图2中,延长CB交x轴于K,则看(2,0).设A(n,0).根据S△ABC=S△AKCS△AKB=3,解方程求出n即可解决问题.
(3)分四种情形:如图31中,当0<t<2时,∠DBE=∠CBD+∠CBE.如图32中,当t=2时,∠DBE=45°或135°.如图33中,当2<t≤6时,∠DBE=∠ABE=∠ABD.如图34中,当t>6时,∠DBE=∠CBE∠CBD,分别求解即可解决问题.
(1)如图1中,
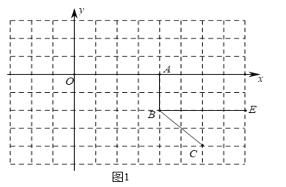
当t=4时,OA=4,
∴A(4,0),
∵B(4,2),
∴AB⊥OA,
∴∠OAB=90°,即m=90.
故答案为90.
![]() 延长
延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
过![]() 作
作![]() 于点
于点![]()
连接![]()
![]()
![]()
设A(n,0).
又S△ABC=S△AKCS△AKB=3
![]()
解得n=5或n=-1(舍去)
![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
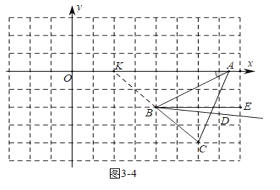
(3)如图31中,当0<t<2时,
∵∠ABC=(180°m°)+(180°45°)=315m°,BD平分∠ABC,
∴∠CBD=![]() ∠ABC=
∠ABC=![]()
∴∠DBE=∠CBD+∠CBE=![]() +45°=
+45°=![]()
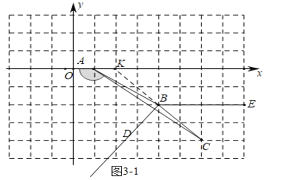
如图32中,当t=2时,∠DBE=45°或135°
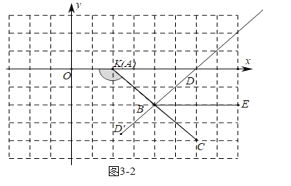
如图33中,当2<t≤6时,
∵OA∥BE,
∴∠ABE=∠OAB=m°,
∴∠ABC=45°+m°,
∵BD平分∠ABC,
∴∠ABD=![]() ,
,
∴∠DBE=∠ABE∠ABD=m°![]() =
=![]()
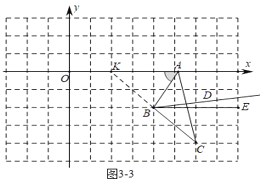
如图34中,当t>6时,同法可得:∠DBE=∠CBE∠CBD=45°![]() =
=![]() ;
;
综上,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.


 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k≠0)的图象经过点(1,﹣k+2).
(k≠0)的图象经过点(1,﹣k+2).
(1)求这个反比例函数的表达式;
(2)若(a,y1),(a+1,y2)是这个反比例函数图象上同一象限内的两个点,请比较y1、y2的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30°,点A1、A2、A3、…在射线ON上,点B1、B2、B3、…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4、…均为等边三角形,若OA1=1,则△A9B9A10的边长为( )
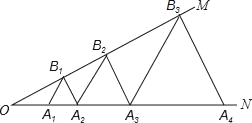
A. 32 B. 64 C. 128 D. 256
查看答案和解析>>
科目:初中数学 来源: 题型:
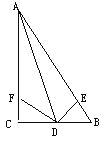
【题目】如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于点E,点F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AB=12,AF=8,求CF的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O在直线MN上,∠AOB=90°,OC平分∠MOB.
(1)若∠AOC=![]() 则∠BOC=_______,∠AOM=_______,∠BON=_________;
则∠BOC=_______,∠AOM=_______,∠BON=_________;
(2)若∠AOC=![]() 则∠BON=_______(用含有
则∠BON=_______(用含有![]() 的式子表示);
的式子表示);
(3)将∠AOB绕着点O顺时针转到图2的位置,其他条件不变,若∠AOC=![]() (
(![]() 为钝角),求∠BON的度数(用含
为钝角),求∠BON的度数(用含![]() 的式子表示).
的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东东玩具商店用500元购进一批悠悠球,很受中小学生欢迎,悠悠球很快售完,接着又用900元购进第二批这种悠悠球,所购数量是第一批数量的1.5倍,但每套进价多了5元.
(1)求第一批悠悠球每套的进价是多少元;
(2)如果这两批悠悠球每套售价相同,且全部售完后总利润不低于25%,那么每套悠悠球的售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的不等式x﹣ ![]() <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
<1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )
A.有两个相等的实数根
B.有两个不相等的实数根
C.无实数根
D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个长为![]() 、宽为
、宽为![]() 的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
的长方形,沿图中虛线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
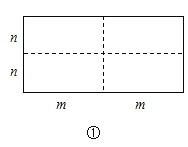
(1)图②中的阴影部分的面积为
(2)观察图②,请你写出代数式![]() 与
与![]() 之间的等量关系式
之间的等量关系式

(3)若![]() 则
则![]()
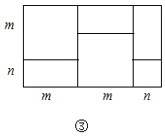
(4)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示
(5)试画出一个几何图形,使它的面积能表示![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com