
分析 先算括号里的减法,把除法变成乘法,进行计算后代入求出即可.
解答 解:$\frac{1}{x-y}$÷($\frac{1}{y}$-$\frac{1}{x}$)
=$\frac{1}{x-y}$÷$\frac{x-y}{xy}$
=$\frac{1}{x-y}$•$\frac{xy}{x-y}$
=$\frac{xy}{(x-y)^{2}}$,
当x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$时,
原式=$\frac{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2})^{2}}$=$\frac{1}{8}$.
点评 此题考查了分式的化简求值问题.此题难度不大,解题的关键是掌握分母有理化的知识.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
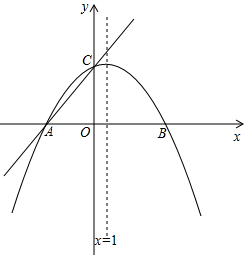 如图,在平面直角坐标系xOy中,一次函数y=$\frac{5}{4}$x+m(m为常数)的图象与x轴交于点A(-3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B
如图,在平面直角坐标系xOy中,一次函数y=$\frac{5}{4}$x+m(m为常数)的图象与x轴交于点A(-3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com