
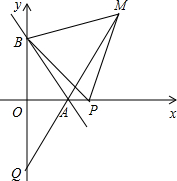
 ��ͼ��ֱ��AB��x���������ڵ�A��a��0������y���������ڵ�B��0��b������a��b���㣨a-b��2+$\sqrt{{b}^{2}-16}$=0
��ͼ��ֱ��AB��x���������ڵ�A��a��0������y���������ڵ�B��0��b������a��b���㣨a-b��2+$\sqrt{{b}^{2}-16}$=0���� ��1�����ݡ����Ǹ����ĺ͵���0������Щ�Ǹ���������0�������a��b��ֵ���Ӷ��ɵõ�A��B��������ꣻ
��2������E��EN��x����N����ͼ1��Ҫ֤��BDO=��EDA��ֻ��֤��END�ס�BOD��ֻ��֤$\frac{EN}{DN}$=$\frac{BO}{DO}$����֤AN=EN����EN=x������AN=x��ON=4-x����֤��ONE�ס�BOD��Ȼ���������������ε����ʿɵõ�����x�ķ��̣�Ȼ�����x�Ϳɽ�����⣻
��3����֤��BAO=��BMP=45�㣬�ɴ˿ɵ�A��P��M��B�ĵ㹲Բ������Բ�ܽǶ����ɵá�MAP=��MBP=45�㣬�����ɵá�OQA=��OAQ=45�㣬���ɵõ�OQ=OA=4��
��� �⣺��1���ߣ�a-b��2+$\sqrt{{b}^{2}-16}$=0��
��a-b=0��b2-16=0��
��a��0��b��0��
��a=b=4��
���A��������4��0������B��������0��4����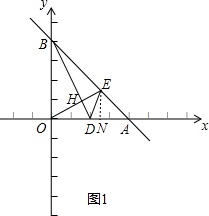
��2������E��EN��x����N����ͼ1��
����EN��OB��
���ANE�ס�AOB��
��$\frac{AN}{NE}$=$\frac{AO}{OB}$=1��
��AN=NE��
��EN=x������AN=x��ON=4-x��
��OE��BD��EN��OA��OA��OB��
���BOD=��ONE=90�㣬��OBD=��NOE=90��-��ODH��
���ONE�ס�BOD��
��$\frac{EN}{DO}$=$\frac{ON}{BO}$��
��$\frac{x}{2}$=$\frac{4-x}{4}$��
��ã�x=$\frac{4}{3}$��
��AN=EN=$\frac{4}{3}$��DN=AD-AN=2-$\frac{4}{3}$=$\frac{2}{3}$��
��$\frac{EN}{DN}$=2=$\frac{BO}{DO}$��
�֡ߡ�BOD=��END=90�㣬
���END�ס�BOD��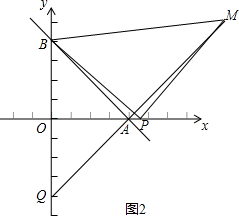
���EDA=��BDO��
��3����ͼ2��
��OA=OB����AOB=90�㣬PB=PM����BPM=90�㣬
���BAO=��BMP=45�㣬
��A��P��M��B�ĵ㹲Բ��
���MAP=��MBP=45�㣬
���OAQ=��MAP=45�㣬
���OQA=90��-45��=45��=��OAQ��
��OQ=OA=4��
�൱��P��x�����˶�ʱ���߶�OQ�ij����䣬����4��
���� ������Ҫ���������������ε��ж������ʡ��ĵ㹲Բ���ж���Բ�ܽǶ��������������ε��ж������ʡ���һԪһ�η��̡��Ǹ�����֪ʶ�������2С��Ĺؼ��ǰ�֤����BDO=��EDAת��Ϊ֤����END�ס�BOD�������3С��Ĺؼ���ͨ��֤��A��P��M��B�ĵ㹲Բ�õ���MAP=��MBP=45�㣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
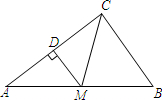 ��ͼ���ڡ�ABC�У���M�ڱ�AB�ϣ�AM=CM��DM��AC����DM��BC��˵����CMB�ǵ��������Σ�
��ͼ���ڡ�ABC�У���M�ڱ�AB�ϣ�AM=CM��DM��AC����DM��BC��˵����CMB�ǵ��������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
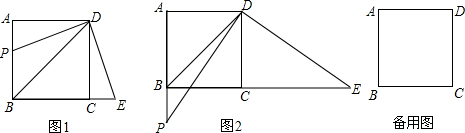
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 120�� | B�� | 135�� | C�� | 150�� | D�� | 165�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com