
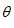 <180 °),得到△ADE ,BD 和EC 所在直线相交于点O.
<180 °),得到△ADE ,BD 和EC 所在直线相交于点O. 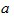 ,当
,当 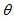 =20 °时,△ABD 与△ACE 是否全等?( )(填“是”或“否”),∠BOE=( )度;
=20 °时,△ABD 与△ACE 是否全等?( )(填“是”或“否”),∠BOE=( )度; C旋转到如图
C旋转到如图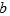 所在位置时,求∠BOE的度数;
所在位置时,求∠BOE的度数; 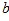 ,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<
,在AB和AC上分别截取点B′和C′,使AB= AB′,AC= AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角 (0°<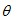 <180°),得到△ADE
<180°),得到△ADE 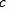 探索∠BOE的度数,直接写出结果,不必说明理由.
探索∠BOE的度数,直接写出结果,不必说明理由.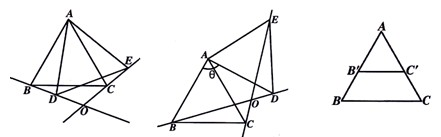
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
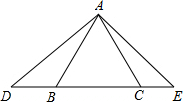 如图,已知△ABC是等边三角形,点D,B,C,E在同一直线上,
如图,已知△ABC是等边三角形,点D,B,C,E在同一直线上,查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知△ABC是等边三角形,点D是AC边上一动点,△BDE是等边三角形,连接AE.
如图,已知△ABC是等边三角形,点D是AC边上一动点,△BDE是等边三角形,连接AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com