

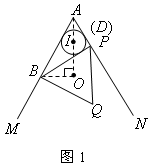
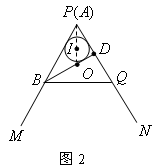
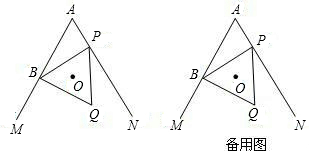
| 解:(1)证明:如图: 连结OB,OP, ∵O是等边三角形BPQ的外心, ∴OB=OP, 圆心角 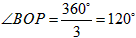 , ,当OB不垂直于AM时,作OH⊥AM,OT⊥AN,垂足分别为H,T, 由 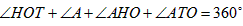 ,且∠A=60°, ,且∠A=60°, , ,∴ 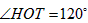 , ,∴  , ,∴  , ,∴OH=OT, ∴点O在∠MAN的平分线上 当  时, 时, , ,即OP⊥AN, ∴点O在∠MAN的平分线上, 综上所述,当点P在射线AN上运动时,点O在∠MAN的平分线上; |
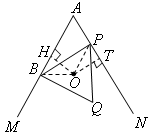 |
| (2)如图: ∵AO平分∠MAN,且∠MAN=60°, ∴  , ,由(1)知,OB=OP,∠BOP=120°, ∴ 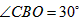 , ,∴ 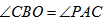 , ,∴  , ,∴  , ,∴ 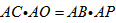 , ,∴y=4x, 定义域为x>0; |
 |
(3)①如图1:当BP与圆I相切时,AO=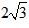 , ,②如图2,当BP与圆I相切时,AO= 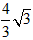 ; ;③如图3,当BQ与圆I相切时,AO=0。 |
   |


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:第35章《圆(二)》中考题集(04):35.2 直线与圆的位置关系(解析版) 题型:解答题
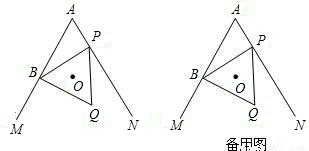
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com