
【题目】如图l,在矩形ABCD中,BC>AB,∠BAD的平分线AF与BD、BC分别交于点E、F,点O是BD的中点,直线OK∥AF,交AD于点K,交BC于点G.
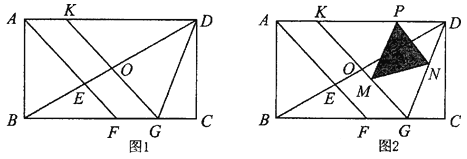
(1)求证:△DOK≌△BOG;
(2)求证:AB+AK=BG:
(3)如图2,若KD=KG=2,点P是线段KD上的动点(不与点D、K重台),PM∥DG交KG于点M,PN∥KG交DG于点N,设PD=x,S△PMN=y,求出y与x的函数关系式.
【答案】(1)证明见解析(2)![]()
【解析】(1)先根据AAS判定△DOK≌△BOG,(2)再根据等腰三角形ABF和平行四边形AFKG的性质,得出结论BG=AB+AK;(3)利用△DKG∽△PKM∽△DPN,由相似三角形的性质求出y与x的函数关系式.
解:(1)∵在矩形ABCD中,AD∥BC
∴∠KDO=∠GBO,∠DKO=∠BGO
∵点O是BD的中点
∴DO=BO
∴△DOK≌△BOG(AAS)
(2)∵四边形ABCD是矩形
∴∠BAD=∠ABC=90°,AD∥BC
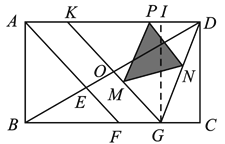
又∵AF平分∠BAD
∴∠BAF=∠BFA=45°
∴AB=BF
∵OK∥AF,AK∥FG
∴四边形AFGK是平行四边形
∴AK=FG
∵BG=BF+FG
∴BG=AB+AK
(3)解法一:
如图,过点G作GI⊥KD于点I,
由(2)知,四边形AFGK是平行四边形,△ABF为等腰直角三角形.
∴AF=KG=2, ![]() .
.
∵四边形ABCD是矩形,
∴GI=AB=![]() ,
,![]() 。
。
∵PD=x
∴PK=2﹣x
∵PM∥DG,PN∥KG
∴四边形PMGN是平行四边形,△DKG∽△PKM∽△DPN
∴ ,
,
即![]()
同理, ![]()
![]()
![]()
![]() .
.
解法二:
如图,过点P作PQ⊥KG于点Q,
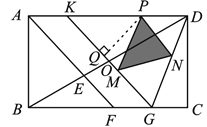
∴KD=KG,∠KDG=∠KGD
又∵PN∥KG
∴∠PND=∠KGD
∴∠PND=∠KDFG
∴PN=PD=x.
∵AF∥KG,
∴∠PKM=∠DAF=45°,又∵PK=2﹣x
∴![]()
又∵PN∥KG,
![]() .
.
“点睛”本题主要考查了矩形的性质以及平行四边形的性质,解题时需要运用全等三角形的判定与性质.解答此题的关键是运用相似三角形的面积之比等于相似比的平方这一性质,并根据图形面积的等量关系列出方程进行求解,难度较大,具有一定的综合性.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:初中数学 来源: 题型:
【题目】某校九年级一班数学调研考试成绩绘制成频数分布直方图,如图(得分取整数).请根据所给信息解答下列问题:
(1)这个班有多少人参加了本次数学调研考试?
(2)60.5~70.5分数段的频数和频率各是多少?
(3)请你根据统计图,提出一个与(1),(2)不同的问题,并给出解答.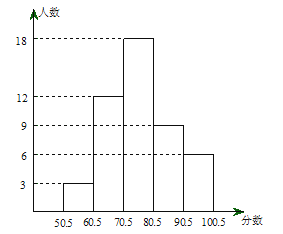
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一面矩形彩旗完全展平时的尺寸图(单位:cm),其中矩形ABCD是由双层白布缝制的穿旗杆用的旗裤,阴影部分DCEF为矩形绸缎旗面.
(1)用经加工的圆木杆穿入旗裤作旗杆,求旗杆的最大直径(精确到1cm);
(2)将穿好彩旗的旗杆垂直插在操场上,旗杆从旗顶到地面的高度为220cm,在无风的天气里,彩旗自然下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场新进一批空调,按进价提高30 %后标价.五一期间,商场为了促销,又按标价打九折销售,每台空调仍可获利680元,该批空调每台的进货价格为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,AB边上的高CD=4.点P从点A出发,沿AB以每秒3个单位长度的速度向终点B运动.当点P不与点A、B重合时,过点P作PQ⊥AB,交边AC或边BC于点Q,以PQ为边向右侧作正方形PQMN.设正方形PQMN与△ABC重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
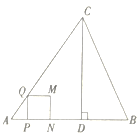
(1)求tanB的值.
(2)求点M落在边BC上时t的值.
(3)当正方形PQMN与△ABC重叠部分为四边形时,求S与t之间的函数关系式.
(4)边BC将正方形PQMN的面积分为两部分时,设这两部分的面积比为k.当![]() 时,直接写出t的取值范围.
时,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com