
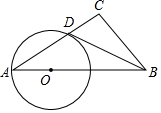
 如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线.
如图,Rt△ABC中∠C=90°,点O是AB边上一点,以OA为半径作⊙O,与边AC交于点D,连接BD,若∠DBC=∠A,求证:BD是⊙O的切线. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
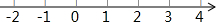 解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x-2≥3(x-1)}\\{\frac{1}{2}x-1<5-\frac{3}{2}x}\end{array}\right.$,并把解集在所给数轴上表示出来.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数 | B. | 方差 | C. | 中位数 | D. | 极差 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
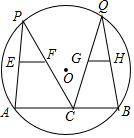 如图,P、Q两点是半径为2cm的⊙O上的两动点,E、F分别是弦PA、PC的中点,G、H分别是弦QC、QB的中点,则EF+GH的值( )
如图,P、Q两点是半径为2cm的⊙O上的两动点,E、F分别是弦PA、PC的中点,G、H分别是弦QC、QB的中点,则EF+GH的值( )| A. | 随着P、Q的运动而变化 | |
| B. | 等于2cm | |
| C. | P、Q两点在弦AB同侧时,EF+GH为定值,在AB异侧时不为定值 | |
| D. | 等于AB的一半 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
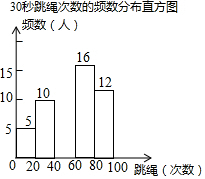 某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:| 成绩段 | 频数 | 频率 |
| 0≤x<20 | 5 | 0.1 |
| 20≤x<40 | 10 | a |
| 40≤x<60 | b | 0.14 |
| 60≤x<80 | m | c |
| 80≤x<100 | 12 | n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com