
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
①2a﹣b=0;
②abc>0;
③4ac﹣b2<0;
④9a+3b+c<0;
⑤关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
⑥8a+c<0.
其中正确的个数是( )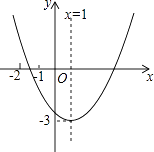
A.2
B.3
C.4
D.5
【答案】C
【解析】解:①抛物线的对称轴为x=﹣ ![]() =1,b=﹣2a,
=1,b=﹣2a,
所以2a+b=0,故①错误;
②抛物线开口向上,得:a>0;抛物线的对称轴为x=﹣ ![]() >0故b<0;抛物线交y轴于负半轴,得:c<0;所以abc>0;故②正确;
>0故b<0;抛物线交y轴于负半轴,得:c<0;所以abc>0;故②正确;
③由图知:抛物线与x轴有两个不同的交点,则△=b2﹣4ac>0,∴4ac﹣b2<0,故③正确;
④根据抛物线的对称轴方程可知:(﹣1,0)关于对称轴的对称点是(3,0);
当x=﹣1时,y<0,所以当x=3时,也有y<0,即9a+3b+c<0;故④正确;
⑤二次函数y=ax2+bx+c的最小值为﹣3,所以关于x的一元二次方程ax2+bx+c+3=0有两个相等的实数根,故⑤正确;
⑥由图知:当x=﹣2时y>0,所以4a﹣2b+c>0,因为b=﹣2a,所以4a+4a+c>0,即8a+c>0,故⑥错误;
所以这结论正确的有②③④⑤4个.
故选C.
【考点精析】根据题目的已知条件,利用二次函数的图象和二次函数的性质的相关知识可以得到问题的答案,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑甲壳虫从点A出发,白甲壳虫从点C1出发,它们以相同的速度分别沿棱向前爬行.黑甲壳虫爬行的路线是:AA1→A1D1→D1C1→C1C→CB→BA→AA1→A1D1…,白甲壳虫爬行的路线是:C1C→CB→BB1→B1C1→C1C→CB…,那么当黑、白两个甲壳虫各爬行完第2018条棱分别停止在所到的正方体顶点处时,它们之间的最短路程的平方是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某风景区内一座塔AB的高度,小明分别在塔的对面一楼房CD的楼底C,楼顶D处,测得塔顶A的仰角为45°和30°,已知楼高CD为10m,求塔的高度(结果精确到0.1m).(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点F,C是⊙O上两点,且 ![]() =
= ![]() =
= ![]() ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D. 
(1)求证:CD是⊙O的切线;
(2)若CD=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中画出直线y=![]() x+1的图象,并根据图象回答下列问题:
x+1的图象,并根据图象回答下列问题:
(1)写出直线与x轴、y轴的交点坐标;
(2)求出直线与坐标轴围成的三角形的面积;
(3)若直线y=kx+b与直线y=![]() x+1关于y轴对称,求k,b的值.
x+1关于y轴对称,求k,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形.则下列下子方法不正确的是【 】.[说明:棋子的位置用数对表示,如A点在(6,3)]

A.黑(3,7);白(5,3) B.黑(4,7);白(6,2)
C.黑(2,7);白(5,3) D.黑(3,7);白(2,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E. 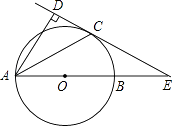
(1)求证:直线CD为⊙O的切线;
(2)当AB=2BE,且CE= ![]() 时,求AD的长.
时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com