
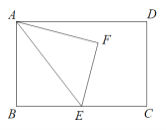
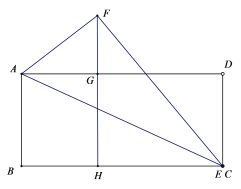
【题目】如图,在矩形ABCD中,AB=10,BC=m,E为BC边上一点,沿AE翻折△ABE,点B落在点F处.
(1)连接CF,若CF//AE,求EC的长(用含m的代数式表示);
(2)若EC=![]() ,当点F落在矩形ABCD的边上时,求m的值;
,当点F落在矩形ABCD的边上时,求m的值;
(3)连接DF,在BC边上是否存在两个不同位置的点E,使得?若存![]() 在,直接写出m的取值范围;若不存在,说明理由.
在,直接写出m的取值范围;若不存在,说明理由.
【答案】(1)EC=![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)由翻折的性质可知BF⊥AE,CF//AE,所以![]() ,根据直角三角形的性质,两锐角互余,可证得EF=EC,所以点E是BC的中点,即可求得EC的长;
,根据直角三角形的性质,两锐角互余,可证得EF=EC,所以点E是BC的中点,即可求得EC的长;
(2)分两种情况进行分类讨论,当点F在AD边上,很容易可证得四边形ABEF是正方形,所以BE=![]() ,就可求出m的值,当点F在CD上,由翻折的性质可得,
,就可求出m的值,当点F在CD上,由翻折的性质可得,![]() ,AB=AF=10,在△ECF中由勾股定理可表示出CF的长,在△ADF中,由勾股定理即可求出m的值;
,AB=AF=10,在△ECF中由勾股定理可表示出CF的长,在△ADF中,由勾股定理即可求出m的值;
(3)由![]() 可知,点F到AD边的距离为5,有两种情况,第一种情况当点F在矩形内,可得
可知,点F到AD边的距离为5,有两种情况,第一种情况当点F在矩形内,可得![]() ,第二种情况当点F在AD边上方,可得
,第二种情况当点F在AD边上方,可得![]() ,要使在BC边上存在两个不同位置的点E,所以
,要使在BC边上存在两个不同位置的点E,所以![]() .
.
(1)连接CF,BF,BF交AE于点H,如下图所示:

∵△ABE沿AE翻折到了△AFE,由翻折可得:
∴BE=EF,BF⊥AE,
∴![]() ,
,
∵CF//AE,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵BE=EF
∴∠BFE=∠FBE
∴∠EFC=∠ECF
∴EF=EC
∴EC=![]() .
.
(2)①当点F在AD上,如下图所示:
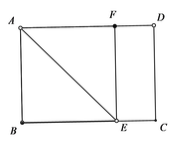
由翻折可得:
AB=AF=10,BE=EF,∠BAE=∠FAE=45![]()
∵四边形ABCD是矩形,
∴∠ABE=90![]() ,AD//BC,
,AD//BC,
∴△ABE是等腰直角三角形,
∴AB=BE=AF=10,
∴四边形ABEF是正方形,
∵EC=![]() ,
,
∴![]() =10
=10
∴![]() ;
;
②当点F在边CD上,如下图所示:
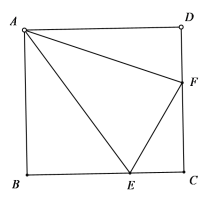
∵EC=![]() ,
,
∴![]()
由翻折可得:
BE=EF,AB=AF=10,
在Rt△ECF中,由勾股定理得:
![]()
∴![]() ,
,
在Rt△ADF中,由勾股定理得:
![]() ,
,
解得:![]()
∴综上所述:![]() 或
或![]() .
.
(3)存在,
过F点作AD的垂线,交AD于G点,设FG为h,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
①当点F再AD的下方,点E和点C重合时,如图所示:
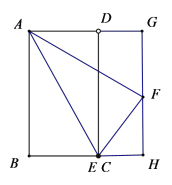
在△AGF中,由勾股定理得:
![]() ,
,
∴![]() ,
,
在△EHF中,由勾股定理得:
![]() ,
,
![]() ,
,
当点F在AD的上方时,点E和点C重合,如图所示:
在△AGF中,由勾股定理得:
![]() ,
,
∴![]() ,
,
在△EHF中,由勾股定理得:
![]() ,
,
![]() ,
,
∴在BC边上存在两个不同位置的点E,![]() ,
,
故答案为:![]() .
.


 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
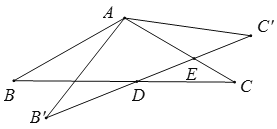
【题目】如图,△ABC中,AB=AC=2,∠B=30°,△ABC绕点A逆时针旋转α(0<α<120°)得到![]() ,
,![]() 与BC,AC分别交于点D,E.设
与BC,AC分别交于点D,E.设![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的函数图象大致为( )
的函数图象大致为( )
A.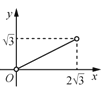 B.
B.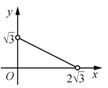 C.
C.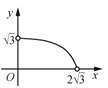 D.
D.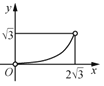
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
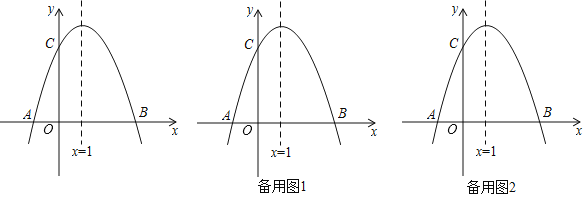
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①若![]() 与
与![]() 相似,请直接写出
相似,请直接写出![]() 的值;
的值;
②![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对该校学生进行了“你喜欢的运动项目”的情况问卷调查,在全部调查问卷中,随机抽取了部分学生的调查问卷进行了分析整理,得到了如下的样本统计图表和扇形统计图:
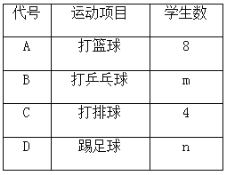
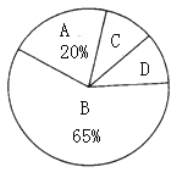
(1)求m,n的值;
(2)该校学生总数为500人,学校决定按比例在B,C,D类学生中抽取学生进行课余训练,其比例为B类20%,C,D类各取60%,请你估计该校参加课余训练的学生数;
(3)随机抽取的部分学生的调查问卷中,若C类运动项目的4位学生中有3位男生,1位女生,请用列举法求出在C类中随机抽出2位学生进行专家培训,其中有1位女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,RtΔABC中∠C=90°,∠ABC=30°,ΔABC绕点C顺时针旋转得ΔA1B1C,当A1落在AB上时,连接B1B,取B1B的中点D,连接A1D,则![]() 的值为_______.
的值为_______.
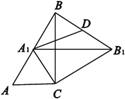
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明投掷一次骰子,向上一面的点数记为![]() ,再投掷一次骰子,向上一面的点数记为
,再投掷一次骰子,向上一面的点数记为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标
的一个坐标![]() ,那么点
,那么点![]() 落在双曲线
落在双曲线![]() 上的概率为( )
上的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com