
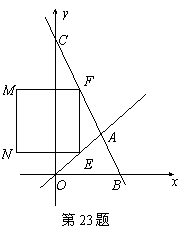
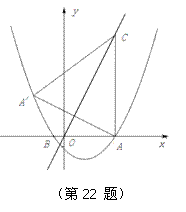
如图,在平面直角坐标系中,两个一次函数y=x,y=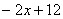 的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
的图象相交于点A,动点E从O点出发,沿OA方向以每秒1个单位的速度运动,作EF∥y轴与直线BC交于点F,以EF为一边向x轴负方向作正方形EFMN,设正方形EFMN与△AOC的重叠部分的面积为S.
(1)求点A的坐标;
(2)求过A、B、O三点的抛物线的顶点P的坐标;
(3)当点E在线段OA上运动时,求出S与运动时间t(秒)的函数表达式;
 (4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.
(4)在(3)的条件下,t为何值时,S有最大值,最大值是多少?此时(2)中的抛物线的顶点P是否在直线EF上,请说明理由.
解:(1)依题意得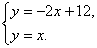 解得
解得
∴点A的坐标为(4,4). …………………………3分
(2)直线y=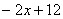 与x轴交点B的坐标为(6,0).
与x轴交点B的坐标为(6,0).
设过A、B、O的抛物线的表达式为y=ax2+bx,
依题意得 解得
解得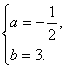
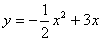 =
= ,∴点P坐标(3,
,∴点P坐标(3,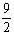 ). ………………6分
). ………………6分
(3)设直线MF、NE与y轴交于点P、Q, 则△OQE是等腰直角三角形.
∵OE=1×t= t, ∴EQ=OQ=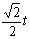 ,∴E(
,∴E(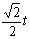 ,
,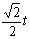 ).
).
∵EF∥y轴, ∴PF=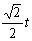 ,
, =12-
=12- .
.
∴EF=PQ=12- -
- =
= .
.
①当EF>QE时, 即 >
>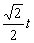 ,解得
,解得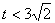 .
.
∴当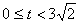 时,
时, (
( )=
)=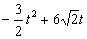 .
.
②当EF≤QE时,即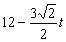 ≤
≤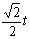 ,解得
,解得 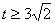 .
.
∴当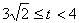
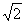 时,S=EF2=(
时,S=EF2=(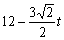 )2 . ………………………10分
)2 . ………………………10分
(4)当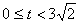 时,
时,  =
= .
.
∴当 时,S最大=12 .
时,S最大=12 .
当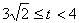
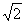 时,S最大=(
时,S最大=(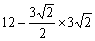 )2=9.
)2=9.
∴当 时,S最大=12. ……………………………11分
时,S最大=12. ……………………………11分
当 时,E(2,2),F(2,8),
时,E(2,2),F(2,8),
∵P(3,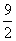 ),∴点P不在直线EF上. ……………………………12分
),∴点P不在直线EF上. ……………………………12分


科目:初中数学 来源: 题型:
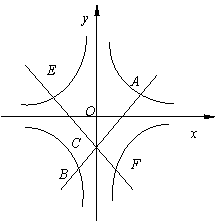
如图,在平面直角坐标系中,双曲线y=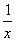 与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y=
与一次函数y=kx+b (k>0)分别交于点A与点B,直线与y轴交于点C,把直线AB绕着点C旋转一定的角度后,得到一条新直线。若新直线与双曲线y= 相交于点E、F,并使得双曲线y=
相交于点E、F,并使得双曲线y= 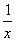 ,y=
,y= ,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小。最小值是多少?
,连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称,如果点A的横坐标为1,则当k为多少时,点A、点E、点B、点F构成的四边形的面积最小。最小值是多少?
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
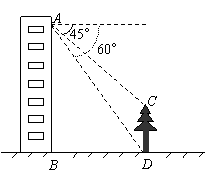
如图,小芸在自家楼房的窗户A处,测量楼前的一棵树CD的高. 现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为20米.请你帮助小芸计算树的高度(精确到0.1米).
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线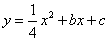 与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x
与x轴交于A(5,0)、B(-1,0)两点,过点A作直线AC⊥x 轴,交直线
轴,交直线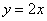 于点C;
于点C;
(1)求该抛物线的解析式;
(2)求点A关于直线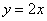 的对称点
的对称点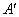 的坐标,判定点
的坐标,判定点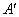 是否在抛物线上,并说明理由;
是否在抛物线上,并说明理由;
(3)点P是抛物线上一动点,过点P作y轴的平行线,交线段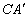 于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
于点M,是否存在这样的点P,使四边形PACM是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com