
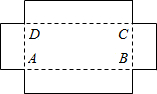
 如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为xcm.
如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为xcm.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为xcm.
如图,用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子,若在铁片的四个角截去四个相同的小正方形,设小正方形的边长为xcm.查看答案和解析>>
科目:初中数学 来源: 题型:
 某工厂生产的边长为1米的正方形装饰材料ABCD如图所示,点E在BC上,点F是CD的中点.△ABE、△CEF和四边形AEFD分别由Ⅰ型、Ⅱ型、Ⅲ型三种材料制成.
某工厂生产的边长为1米的正方形装饰材料ABCD如图所示,点E在BC上,点F是CD的中点.△ABE、△CEF和四边形AEFD分别由Ⅰ型、Ⅱ型、Ⅲ型三种材料制成.查看答案和解析>>
科目:初中数学 来源: 题型:
 现有一段旧围墙长20米,李叔叔想紧靠这段围墙圈一块长方形空地作为兔舍饲养
现有一段旧围墙长20米,李叔叔想紧靠这段围墙圈一块长方形空地作为兔舍饲养查看答案和解析>>
科目:初中数学 来源: 题型:
列方程(组)解应用题:
如图是一块长、宽分别为60 m、50 m的矩形草坪,草坪中有宽度均为x m的一横两纵的甬道.

1.用含x的代数式表示草坪的总面积S ;
2.当甬道总面积为矩形总面积的![]() %时,求甬道的宽
%时,求甬道的宽
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com