
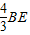 +CF=AB;
+CF=AB;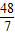 ,GF:AC=4
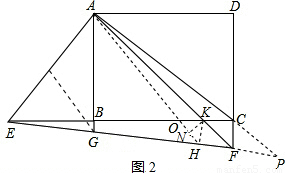
,GF:AC=4 :7,求KH的长.
:7,求KH的长.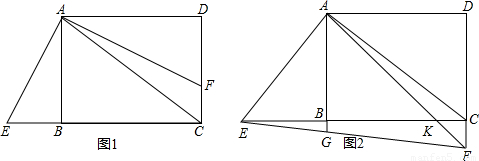
 BE进而求出
BE进而求出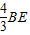 +CF=AB;
+CF=AB; =
=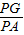 =
=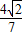 ,再证明△PAG∽△PEA,求出AE的长,进而得出△AOK∽△EOH和△AOE∽△KOH,得出∠AEO=∠KHO=45°,
,再证明△PAG∽△PEA,求出AE的长,进而得出△AOK∽△EOH和△AOE∽△KOH,得出∠AEO=∠KHO=45°,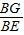 =
=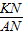 =
=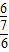 =
= ,求出KN即可得出HK的长.
,求出KN即可得出HK的长.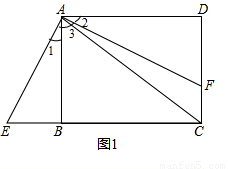 (1)∵AF⊥AE,
(1)∵AF⊥AE,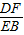 =
= ,
, BE,
BE,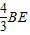 +CF=AB;
+CF=AB;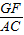 =
=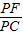 ,
,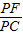 =
= ,
,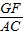 =
=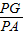 =
=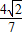 ,
,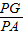 =
=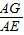 ,
, =
=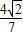 ,
, =
=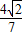 ,
,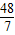 ,
,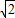 ,
,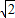 ,AG=
,AG=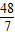 ,tan∠AEG=
,tan∠AEG= ,可以得到∠EAB=45°,
,可以得到∠EAB=45°, ,
,
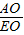 =
=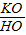 ,
,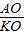 =
=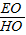 ,
,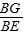 =
=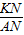 =
=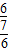 =
= ,
,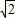 ,
,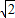 )2=(7x)2+x2,
)2=(7x)2+x2, ,
,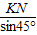 =
=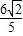 .
.

科目:初中数学 来源: 题型:
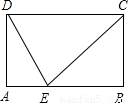
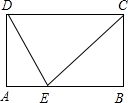 如图,在矩形ABCD中,AD=a,AB=b,问:能否在Ab边上找一点E,使E点与C、D的连线将此矩形分成三个彼此相似的三角形?若能找到,这样的E点有几个?若不能找到,请说明理由.
如图,在矩形ABCD中,AD=a,AB=b,问:能否在Ab边上找一点E,使E点与C、D的连线将此矩形分成三个彼此相似的三角形?若能找到,这样的E点有几个?若不能找到,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

| 3 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
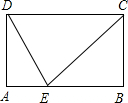 如图,在矩形ABCD中,AD=a,AB=b,问:能否在Ab边上找一点E,使E点与C、D的连线将此矩形分成三个彼此相似的三角形?若能找到,这样的E点有几个?若不能找到,请说明理由.
如图,在矩形ABCD中,AD=a,AB=b,问:能否在Ab边上找一点E,使E点与C、D的连线将此矩形分成三个彼此相似的三角形?若能找到,这样的E点有几个?若不能找到,请说明理由.查看答案和解析>>
科目:初中数学 来源:2011年1月江西省南昌市三校联考九年级数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com