
| A. | y=2x-1 | B. | y=-x+3 | C. | y=$\frac{1}{2}$x+2 | D. | y=2x |
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
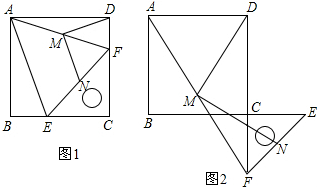
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
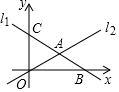 如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{3}$x交于点A.
如图,在平面直角坐标系中,直线l1:y=-$\frac{1}{2}$x+8分别与x轴、y轴交于点B、C,且与直线l2:y=$\frac{1}{3}$x交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
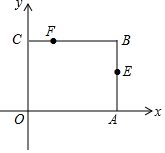 如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
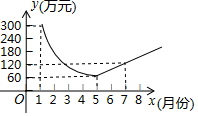 为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )
为了建设生态丽水,某工厂在一段时间内限产并投入资金进行治污改造,下列描述的是月利润y(万元)关于月份x之间的变化关系,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,则下列说法不正确的是( )| A. | 5月份该厂的月利润最低 | |
| B. | 治污改造完成后,每月利润比前一个月增加30万元 | |
| C. | 治污改造前后,共有6个月的月利润不超过120万元 | |
| D. | 治污改造完成后的第8个月,该厂月利润达到300万月 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 区县 | 大兴 | 通州 | 平谷 | 顺义 | 怀柔 | 门头沟 | 延庆 | 昌平 | 密云 | 房山 |
| 最高气温 | 32 | 32 | 30 | 32 | 30 | 32 | 29 | 32 | 30 | 32 |
| A. | 32 | B. | 31 | C. | 30 | D. | 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
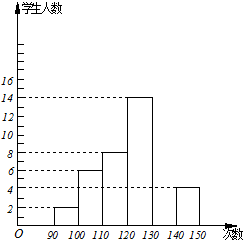 某学校为了了解八年级500名男生体能的情况,从中随机抽取了部分男生进行1分钟跳绳次数测试,将数据整理后,绘制成如下不完整的频数分布表和频数分布直方图:
某学校为了了解八年级500名男生体能的情况,从中随机抽取了部分男生进行1分钟跳绳次数测试,将数据整理后,绘制成如下不完整的频数分布表和频数分布直方图:| 分组 | 频数 | 频率 |
| 90≤x<100 | 2 | 0.04 |
| 100≤x<110 | 6 | 0.12 |
| 110≤x<120 | 8 | b |
| 120≤x<130 | 14 | 0.28 |
| 130≤x<140 | a | 0.32 |
| 140≤x<150 | 4 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
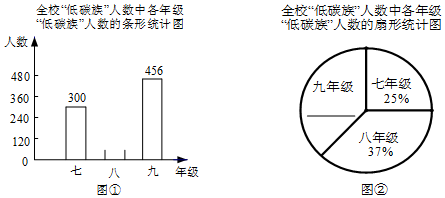
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com