
【题目】某批发商计划将一批海产品由A地运往B地.汽车货运公司和铁路货运公司均开办海产品运输业务.已知运输路程为120千米,汽车和火车的速度分别为60千米/时、100千米/时.两货运公司的收费项目及收费标准如下表所示:
运输工具 | 运输费单价/ (元/吨·千米) | 冷藏费单价/ (元/吨·小时) | 过路费/元 | 装卸及管理费/元 |
汽 车 | 2 | 5 | 200 | 0 |
火 车 | 1.8 | 5 | 0 | 1600 |
注:“元/吨·千米”表示每吨货物每千米的运费;“元/吨·小时”表示每吨货物每小时的冷藏费.
(1)设该批发商待运的海产品有x(吨),汽车货运公司和铁路货运公司所要收取的费用分别为y1(元)和y2(元),试求y1、y2与x之间的函数关系式.
(2)若该批发商待运的海产品不少于30吨,为节省运费,他应选择哪个货运公司承担运输业务?
 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列方程:
(1)2x2-8x=0;
(2)x2-3x-4=0.
求出抛物线的开口方向、对称轴、顶点坐标.
(3)y=![]() x2-x+3(公式法).
x2-x+3(公式法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可以随机抽取一张奖券,抽得奖券“紫气东来”、“化开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元,小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:
奖券种类 | 紫气东来 | 化开富贵 | 吉星高照 | 谢谢惠顾 |
出现张数(张) | 500 | 1000 | 2000 | 6500 |
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更合算?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边AD在x轴上,点B在第四象限,直线BD与反比例函数![]() 的图象交于点B、E.
的图象交于点B、E.
(1)求反比例函数及直线BD的解析式;
(2)求点E的坐标;
(3)连结![]() 、
、![]() 、
、![]() ,求△
,求△![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形的绿地,量得两直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
如图,BD⊥AC,EF⊥AC,D、F分别为垂足,且∠1=∠4,求证:∠ADG=∠C

证明:∵BD⊥AC,EF⊥AC
∴∠2=∠3=90°
∴BD∥EF ( )
∴∠4=_____ ( )
∵∠1=∠4
∴∠1=_____
∴DG∥BC ( )
∴∠ADG=∠C( )
查看答案和解析>>
科目:初中数学 来源: 题型:
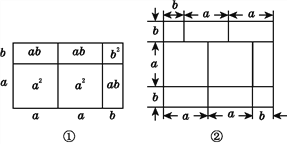
【题目】先阅读再解答:我们已经知道,根据几何图形的面积关系可以说明完全平方公式,实际上还有一些等式也可以用这种方式加以说明,例如:
(2a+b)(a+b)=2a2+3ab+b2,就可以用图①的面积关系来说明.
(1)根据图②写出一个等式: ;
(2)已知等式:(x+p)(x+q)=x2+(p+q)x+pq,请你画出一个相应的几何图形加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
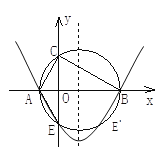
【题目】如图,在Rt△ABC中,∠ACB=90°,BC>AC,以斜边AB 所在直线为x轴,以斜边AB上的高所在直线为y轴,建立直角坐标系,若OA2+OB2= 17, 且线段OA、OB的长度是关于x的一元二次方程x2-mx+2(m-3)=0的两个根.
(1)求C点的坐标;
(2)以斜边AB为直径作圆与y轴交于另一点E,求过A、B、E 三点的抛物线的关系式,并画出此抛物线的草图.
(3)在抛物线上是否存在点P,使△ABP与△ABC全等?若存在,求出符合条件的P点的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com