
【题目】数轴上O,A两点的距离为4,一动点P从点A出发,按以下规律跳动:第1次跳动到AO的中点A1处,第2次从A1点跳动到A1O的中点A2处,第3次从A2点跳动到A2O的中点A3处,按照这样的规律继续跳动到点A4,A5,A6,…,An.(n≥3,n是整数)处,那么线段AnA的长度为________(n≥3,n是整数).

科目:初中数学 来源: 题型:
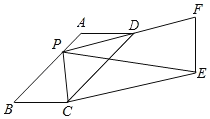
【题目】如图,已知平行四边形ABCD中,∠B=60°,AB=12,BC=5,P为AB上任意一点(可以与A、B重合),延长PD到F,使得DF=PD,以PF、PC为边作平行四边形PCEF,则PE长度的最小值____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮在课余时间写了三个算式:![]() ,
,![]() ,
,![]() ,通过认真观察,发现任意两个连续奇数的平方差是
,通过认真观察,发现任意两个连续奇数的平方差是![]() 的倍数.
的倍数.
验证
(1)![]() 的结果是
的结果是![]() 的几倍?
的几倍?
(2)设两个连续奇数为![]() ,
,![]() (其中
(其中![]() 为正整数),写出它们的平方差,并说明结果是
为正整数),写出它们的平方差,并说明结果是![]() 的倍数;
的倍数;
延伸
直接写出两个连续偶数的平方差是几的倍数.
查看答案和解析>>
科目:初中数学 来源: 题型:
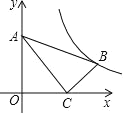
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点A.C的坐标分别是(0,3)、(4,0).∠ACB=90,AC=2BC,则函数y=![]() (k>0,x>0)的图象经过点B,则k的值为( )
(k>0,x>0)的图象经过点B,则k的值为( )
A.10B.11C.12D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
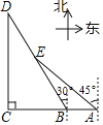
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四张大小、形状都相同的卡片上分别写有数字1,2,3,4,把它们放入不透明的盒子中摇匀.
(1)从中随机抽出1张卡片,抽出的卡片上的数字恰好是偶数的概率为 .
(2)从中随机抽出1张卡片,记录数字后放回摇匀,再抽出一张卡片,记录数字.用树状图或列表法求两次抽出的卡片上的数字恰好是两个相邻整数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
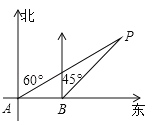
【题目】如图,大海中某灯塔P周围10海里范围内有暗礁,一艘海轮在点A处观察灯塔P在北偏东60°方向,该海轮向正东方向航行8海里到达点B处,这时观察灯塔P恰好在北偏东45°方向.如果海轮继续向正东方向航行,会有触礁的危险吗?试说明理由.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0).
(1)若b=1,a=﹣![]() c,求证:二次函数的图象与x轴一定有两个不同的交点;
c,求证:二次函数的图象与x轴一定有两个不同的交点;
(2)若a![]() 0,c=0,且对于任意的实数x,都有y
0,c=0,且对于任意的实数x,都有y![]() 1,求4a+b2的取值范围;
1,求4a+b2的取值范围;
(3)若函数图象上两点(0,y1)和(1,y2)满足y1y2>0,且2a+3b+6c=0,试确定二次函数图象对称轴与x轴交点横坐标的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com