
分析 (1)先求出方程的两个根,由已知条件即可得出k的取值范围;
(2)分两种情况:①若A(2k,0),B(2,0),由OM=OB得出方程|4k|=2,解方程即可;
②若B(2k,0),A(2,0),得出方程|4k|=|2k|,解方程即可.
解答 解:(1)∵x2-2(k+1)x+4k=0,
∴(x-2)(x-2k)=0,
∴x1=2k,x2=2,
又∵-$\frac{3}{2}$<x1<$\frac{1}{2}$,
∴-$\frac{3}{2}$<2k<$\frac{1}{2}$,即-$\frac{3}{4}$<k<$\frac{1}{4}$;
(2)分两种情况:
①若A(2k,0),B(2,0),
∴OB=2,
又∵M在y轴上,
∴点M的坐标(0,4k),
∴OM=|4k|,
又∵OM=OB,
∴|4k|=2,
解得:k=±$\frac{1}{2}$,
又∵-$\frac{3}{4}$<k<$\frac{1}{4}$,
∴k=-$\frac{1}{2}$;
②若B(2k,0),A(2,0),
则|4k|=|2k|,
解得:k=0;
综上所述:若OM=OB,k的值为-$\frac{1}{2}$或0.
点评 本题考查了一元二次方程的根、抛物线与x轴的交点特征;本题有一定难度,特别是(2)中,需要进行分类讨论,避免漏解.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
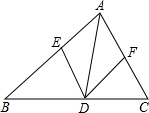 如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )
如图,在△ABC中,点D、E、F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列结论:①四边形AEDF是平行四边形;②如果∠BAC=90°,那么四边形AEDF是矩形;③如果AD平分∠BAC,那么四边形AEDF是菱形;④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形,你认为正确的是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
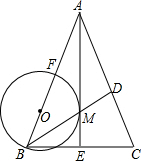 如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.
如图,在△ABC中,AB=AC,角平分线AE,BD相交于M,点O在AB边上,以OB为半径的圆恰好经过点M,且与AB相交于另一点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )
已知AD∥BC,AB⊥AD,点E点F分别在射线AD,射线BC上,若点E与点B关于AC对称,点E点F关于BD对称,AC与BD相交于点G,则( )| A. | ∠AEB+22°=∠DEF | B. | 1+tan∠ADB=$\sqrt{2}$ | C. | 2BC=5CF | D. | 4cos∠AGB=$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.1×10-6西弗 | B. | 3.1×106西弗 | C. | 3.1×10-3西弗 | D. | 3.1×103西弗 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.293×10-3 | B. | -1.293×103 | C. | -12.93×10-2 | D. | 0.1293×10-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com