
 矩形各内角的平分线若能围成一个四边形,则这个四边形一定是C,并证明.
矩形各内角的平分线若能围成一个四边形,则这个四边形一定是C,并证明.分析 因为矩形的四个角都是直角,并由角平分线得出∠HBC=∠HCB=45°,根据三角形的内角可得∠H=90°,同理可得四边形EFGH的其它各角也是90°,所以四边形EFGH为矩形,再证明EH=GH,则矩形EFGH是正方形.
解答 解:矩形各内角的平分线若能围成一个四边形,则这个四边形一定是正方形,理由是:
∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,AB=CD,
∵BH、CH分别是∠ABC、∠BCD的角平分线,
∴∠HBC=∠HCB=45°,
∴∠H=90°,
同理得∠F=∠AEB=90°,
∴∠FEH=90°,
∴四边形EFGH为矩形,
∵∠HBC=∠HCB=45°,
∴BH=CH,
在△ABE和△DCG中,
∵$\left\{\begin{array}{l}{∠BAE=∠CDG=45°}\\{AB=CD}\\{∠ABE=∠DCG=45°}\end{array}\right.$,
∴△ABE≌△DCG(ASA),
∴BE=CG,
∴BH-BE=CH-CG,
即EH=GH,
∴矩形EFGH是正方形;
故选B.
点评 本题考查了矩形的性质和判定、正方形的判定,同时说明了矩形各内角平分线所围成的四边形是正方形;做好此题要熟练掌握矩形的性质,尤其是角的特殊性:矩形的四个角都是直角.


 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
已知,A,B 两市相距 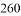 千米,甲车从 A 市前往 B 市运送物资,行驶
千米,甲车从 A 市前往 B 市运送物资,行驶  小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过
小时在 M 地汽车出现故障,立即通知技术人员乘乙车从 A 市赶来维修(通知时间忽略不计),乙车到达 M 地后又经过  分钟修好甲车后以原速原路返回,同时甲车以原速
分钟修好甲车后以原速原路返回,同时甲车以原速 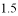 倍的速度前往 B 市,如图是两车距 A 市的路程
倍的速度前往 B 市,如图是两车距 A 市的路程  (千米)与甲车行驶时间
(千米)与甲车行驶时间  (小时)之间的函数图象,结合图象回答下列问题:
(小时)之间的函数图象,结合图象回答下列问题:
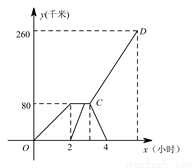
(1)直接写出甲车提速后的速度、乙车的速度、点  的坐标;
的坐标;
(2)求乙车返回时  与
与  的函数关系式并直接写出自变量
的函数关系式并直接写出自变量  的取值范围;
的取值范围;
(3)求甲车到达 B 市时乙车已返回 A 市多长时间?
查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:单选题
甲安装队为 A小区安装  台空调,乙安装队为 B小区安装
台空调,乙安装队为 B小区安装  台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装
台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装  台,设乙队每天安装
台,设乙队每天安装  台,根据题意,下面所列方程中正确的是
台,根据题意,下面所列方程中正确的是 
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,等腰Rt△ABC,∠BAC=90°,A点的坐标为(2,0),过B点的双曲线y=$\frac{k}{x}$(x>0)恰好经过BC的中点D,则k的值是8.
如图,等腰Rt△ABC,∠BAC=90°,A点的坐标为(2,0),过B点的双曲线y=$\frac{k}{x}$(x>0)恰好经过BC的中点D,则k的值是8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在等腰直角三角形ABO中,∠AOB=90°,OA=OB,且AB∥x轴,AB与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点C,BC2-AC2=4,则k的值是-1.
如图,在等腰直角三角形ABO中,∠AOB=90°,OA=OB,且AB∥x轴,AB与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点C,BC2-AC2=4,则k的值是-1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com