
 如图,在?ABCD中,F是CD的中点,延长AB到点E,使BE=$\frac{1}{2}$AB,连接CE,BF.
如图,在?ABCD中,F是CD的中点,延长AB到点E,使BE=$\frac{1}{2}$AB,连接CE,BF.分析 (1)根据平行四边形的性质得到AB∥CD,且AB=DC.由F是CD的中点,得到CF=$\frac{1}{2}$CD.根据平行四边形的判定定理即可得到结论;
(2)如图,过点C作CH⊥BE于点H.解直角三角形得到BH=$\frac{1}{2}$CB=3,CH=3$\sqrt{3}$,根据勾股定理即可得到结论.
解答  证明:(1)在?ABCD中,AB∥CD,且AB=DC.
证明:(1)在?ABCD中,AB∥CD,且AB=DC.
∵F是CD的中点,
∴CF=$\frac{1}{2}$CD.
又∵BE=$\frac{1}{2}$AB,
∴CF=BE,且CF∥BE,
∴四边形BECF是平行四边形;
(2)解:如图,过点C作CH⊥BE于点H.
在?ABCD中,∵∠A=60°,
∴∠CBE=60°.
∵AB=10,AD=6,
∴CB=AD=6,
∴BH=$\frac{1}{2}$CB=3,CH=3$\sqrt{3}$.
在?BECF中,BE=CF=$\frac{1}{2}$CD=5,则EH=2.
∴在Rt△CHE中,根据勾股定理知CE=$\sqrt{(3\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{31}$.
点评 本题考查了平行四边形的判定与性质、勾股定理.平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
 若实数a、b在数轴上对应点的位置如图所示,则$\sqrt{{a}^{2}-2ab+{b}^{2}}$可化简为( )
若实数a、b在数轴上对应点的位置如图所示,则$\sqrt{{a}^{2}-2ab+{b}^{2}}$可化简为( )| A. | a+b | B. | a-b | C. | b-a | D. | -a-b |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解我国各地中学多媒体的使用情况 | |
| B. | 测试我国某新型导弹的威力 | |
| C. | 对某商场防火安全的调查 | |
| D. | 对今年全国各地酒店“杜绝浪费,提倡节约”的调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M.若S正方形ABCD=2,则正方形DEFG的面积为( )
如图,正方形ABCD和正方形DEFG的顶点A在y轴上,顶点D,F在x轴上,点C在DE边上,反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点B、C和边EF的中点M.若S正方形ABCD=2,则正方形DEFG的面积为( )| A. | $\frac{10}{3}$ | B. | $\frac{32}{9}$ | C. | 4 | D. | $\frac{15}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
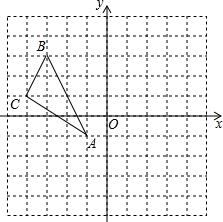 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1)
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-1),B(-3,3),C(-4,1)查看答案和解析>>
科目:初中数学 来源:2017届湖北省九年级三月月考数学试卷(解析版) 题型:判断题
如图,抛物线  交
交  轴于点
轴于点  和点
和点  ,交
,交  轴于点
轴于点  .
.
(1)求抛物线的函数表达式;
(2)若点  在抛物线上,且
在抛物线上,且  ,求点
,求点  的坐标;
的坐标;
(3)如图 b,设点  是线段
是线段  上的一动点,作
上的一动点,作  轴,交抛物线于点
轴,交抛物线于点  ,求线段
,求线段  长度的最大值.
长度的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com