练习册

  • 练习册
  • 试题
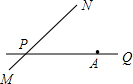    精英家教网 > 初中数学 > 题目详情
    17、若m+n=7，mn=12，则m2-mn+n2的值是
    13
    ．
    分析：做此题时，要有已知条件入手，把m+n=7两边同时平方，就可以出现m2+n22mn的形式，再把等式进行变形，求出m2+n2的值后，再求m2-mn+n2的值即可．
    解答：解：∵m+n=7，
    ∴（m+n）2=72，
    m2+n2+2mn=49，
    ∵mn=12，
    ∴m2+n2，
    =49-2mn，
    =49-2×12，
    =49-24，
    =25，
    ∴m2-mn+n2=25-mn=25-12=13．
    点评：此题主要考查了完全平方公式的变形，有一定综合性，计算应多注意．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，公路PQ和公路MN交于点P，且∠NPQ=30°，公路PQ上有一所学校A，AP=160米，若有一拖拉机沿MN方向以18米∕秒的速度行驶并对学校产生影响，假设拖拉机行驶时周围100米以内会受到噪声的影响，则造成影响的时间为
     
    秒．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    16、若m＜0，mn＜0，则|n-m+1|-|m-n-5|的值是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    6、若△MNP≌△MNQ，且MN=8，NP=7，PM=6，则MQ的长为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，⊙O中半径OA=2，∠AOB=60°，P为
    AB
    上的点，PM⊥OA于M，精英家教网PN⊥OB于N．
    （1）若P是
    AB
    的中点，求MN的长；
    （2）若点P不是
    AB
    的中点，则MN的长度是否发生变化？请说明理由；
    （3）若∠AOB=45°，求MN的长．（不用证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•桂平市三模）如图，直线AC∥BD，⊙O与AC和BD分别相切于点A和点B．点M和点N分别是AC和BD上的动点，MN沿AC和BD平移．⊙O的半径为1，∠1=60°．下列结论错误的是（　　）

    查看答案和解析>>

    同步练习册答案