
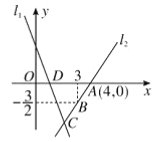
【题目】如图,直线![]() 的解析表达式为
的解析表达式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,直线
,直线![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的解析表达式;
的解析表达式;
(3)在![]() 轴上求作一点
轴上求作一点![]() ,使
,使![]() 的和最小,直接写出
的和最小,直接写出![]() 的坐标.
的坐标.
【答案】(1)D(1,0);(2)y=![]() x6;(3)
x6;(3)![]() (
(![]() ,0).
,0).
【解析】
(1)已知l1的解析式,令y=0求出x的值即可;
(2)设l2的解析式为y=kx+b,代入A、B坐标求出k,b的值即可;
(3)作点B关于x轴的对称点B’, 连接B’C交x轴于M,则点M即为所求,联立解析式可求出点C坐标,然后求出直线B’C的解析式,令y=0求出x的值即可.
解:(1)由y=3x+3,令y=0,得3x+3=0,
解得:x=1,
∴D(1,0);
(2)设直线l2的表达式为y=kx+b,
由图象知:A(4,0),B(3,![]() ),代入表达式y=kx+b,
),代入表达式y=kx+b,
得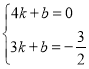 ,解得:
,解得: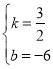
∴直线l2的解析表达式为y=![]() x6;
x6;
(3)作点B关于x轴的对称点B’,则B’的坐标的为(3,![]() ),连接B’C交x轴于M,则点M即为所求,
),连接B’C交x轴于M,则点M即为所求,
联立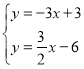 ,解得:
,解得:![]() ,
,
∴C(2,-3),
设直线B’C的解析式为:y=mx+n,代入B’(3,![]() ),C(2,-3),
),C(2,-3),
得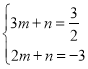 ,解得:
,解得: ,
,
∴直线B’C的解析式为:y=![]() x12,
x12,
令y=0,即![]() x12=0,
x12=0,
解得:![]() ,
,
∴![]() 的坐标为(
的坐标为(![]() ,0).
,0).


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,A(1,0),C(0,2),双曲线y=![]() (0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF,则k值为_____.
(0<k<2)的图象分别交AB,CB于点E,F,连接OE,OF,EF,S△OEF=2S△BEF,则k值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF,
(1)证明:CF=EB.
(2)证明:AB=AF+2EB.
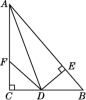
查看答案和解析>>
科目:初中数学 来源: 题型:
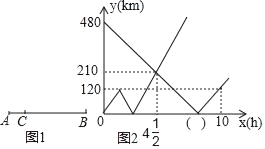
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由C站驶往A地,到达A地后立即原速驶往B地,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象,请结合图象信息解答下列问题:
(1)A,B两地间的距离是 千米;请直接在图2中的括号内填上正确数字;
(2)求货车由B地驶往A地过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(3)客、货两车出发多长时间,距各自出发地的距离相等?直接写出答案;
(4)客、货两车出发多长时间,相距500千米?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线L:y=ax2+bx+c(a,b,c是常数,且abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称此抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
(1)若“路线”l的表达式为y=﹣x+2,它的“带线”L的顶点在反比例函数y=![]() 的图象上,求“带线”L的表达式;
的图象上,求“带线”L的表达式;
(2)如果抛物线y=mx2﹣2mx+m﹣1与直线y=nx+1具有“一带一路”关系,求m,n的值;
(3)设(2)中的“带线”L与它的“路线”l在y轴上的交点为A.已知点P为“带线”L上的点,当以点P为圆心的圆与“路线”l相切于点A时,求出点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展读书月活动,对学生最喜欢的图书种类进行了一次抽样调查,所有图书分成四类:艺术、文学、科普、其他.随机调查了该校m名学生(每名学生必选且只能选择一类图书),并将调查结果制成如下两幅不完整的统计图:
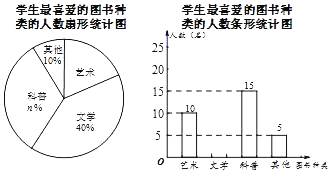
根据统计图提供的信息,解答下列问题:
(1)m= ,n= ,并请根据以上信息补全条形统计图;
(2)扇形统计图中,“艺术”所对应的扇形的圆心角度数是 度;
(3)根据抽样调查的结果,请你估计该校900名学生中有多少学生最喜欢科普类图书.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,BD⊥AD,∠A=45°,E、F分别是AB,CD上的点,且BE=DF,连接EF交BD于O.

(1)求证:BO=DO;
(2)若EF⊥AB,延长EF交AD的延长线于G,当FG=1时,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
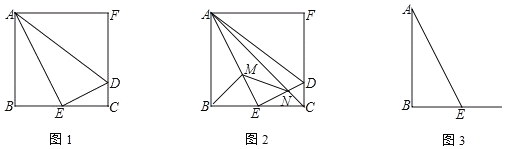
【题目】已知:正方形ABCF中,E为BC中点,点D在CF上,AB=4,CD=1.
(1)判断△AED的形状,并证明;
(2)AC交DE于点N,M在AE上,且满足BM2﹣ME2=EN2﹣CN2,求证:BM⊥AC;
(3)若△APE是以AE为斜边的等腰直角三角形,直接写出BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com