
 如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$.
如图,在△ABC中,点D在AB上,过点D作DF⊥AB交BC于E,交AC延长线于F,DE=AB,EF=BD,若BE=1,则AF的长为$\sqrt{2}$. 分析 过B作BH⊥AB,过E作EH⊥DF,BH,EH交于H,连接AH,HF,得到四边形DBHE是矩形,由矩形的性质得到BH=DE=AB,EH=BD=EF,证得△ABH与△EFH是等腰直角三角形,于是得到∠FHE=∠AHB=45°,HF2=2EF2,AH2=2AB2求出∠AHF=90°,根据勾股定理得到AH2=2DE2=2(BE2-BD2)=2(1-EF2),AF2=AH2+HF2=2(1-EF2)+2EF2=2,等量代换即可得到结论.
解答  解:过B作BH⊥AB,过E作EH⊥DF,BH,EH交于H,连接AH,HF,
解:过B作BH⊥AB,过E作EH⊥DF,BH,EH交于H,连接AH,HF,
∵DF⊥AB,
∴四边形DBHE是矩形,
∴BH=DE=AB,EH=BD=EF,
∴△ABH与△EFH是等腰直角三角形,
∴∠FHE=∠AHB=45°,HF2=2EF2,AH2=2AB2
∴∠AHF=90°,
∵DE=AB,
∴AH2=2DE2=2(BE2-BD2)=2(1-EF2),
∴AF2=AH2+HF2=2(1-EF2)+2EF2=2,
∴AF=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了等腰直角三角形的判定和性质,矩形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
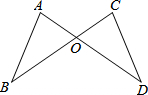 如图,AB=CD,AD=CB,求证:∠A=∠C.小丽的思考过程如下:∵$\left\{\begin{array}{l}{AB=CD}\\{AO=CO}\\{BO=OD}\end{array}\right.$,∴△ABO≌△CDO,∴∠A=∠C
如图,AB=CD,AD=CB,求证:∠A=∠C.小丽的思考过程如下:∵$\left\{\begin{array}{l}{AB=CD}\\{AO=CO}\\{BO=OD}\end{array}\right.$,∴△ABO≌△CDO,∴∠A=∠C查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.
如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=8,BC=3,运动过程中,点D到点O的最大距离为9.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 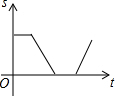 | B. | 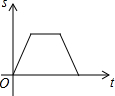 | C. | 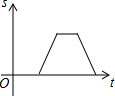 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
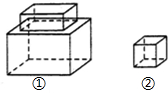 某玩具加工厂要制造如图所示的两种形状的玩具配件,其中,配件①是由大、小两个长方体构成的,大长方体的长、宽、高分别为:$\frac{5}{2}$a、2a、$\frac{3}{2}$a,小长方体的长、宽、高分别为:2a、a、$\frac{a}{2}$;配件②是一个正方体,其边长为a
某玩具加工厂要制造如图所示的两种形状的玩具配件,其中,配件①是由大、小两个长方体构成的,大长方体的长、宽、高分别为:$\frac{5}{2}$a、2a、$\frac{3}{2}$a,小长方体的长、宽、高分别为:2a、a、$\frac{a}{2}$;配件②是一个正方体,其边长为a查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com