
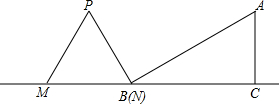
���� ��1���������ɵó�BC��AB����PMN�ĸߵij���������֪��P���A�غ�ʱC����MN�е��ϣ��ɴ˿ɵõ�t��ֵ��
��2�����ͼ�ε��ص���з������ۣ��ֳ�0��t��4��4��t��6��6��t��8��8��t��10����������ǣ��������������ν�����ı߶���t��ʾ���Ϳ������������ϵʽ��
��3����DEMΪ����������ʱ��ΪMλ��DE��ֱƽ������ʱ����������DE�ij��Ϳ������t��ֵ��
��� ��1���ߡ�ACB=90���ABC=30��AC=2$\sqrt{3}$��
��BC=6 AB=4$\sqrt{3}$
�ߡ�PMNΪ�ȱ������Σ�MN=4��
���PMN�ĸ�Ϊ2$\sqrt{3}$��
�൱P��A�غ�ʱCΪMN�е㣨��ͼ1��ʾ����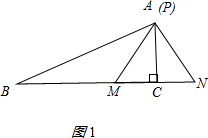
��BN=8��
���P����غ�ʱt=8��
��2�����������
��0��t��4ʱ����ͼ2��ʾ����FE��MN�ڵ�E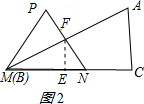
�ߡ�ABC=30�㣬��PMNΪ�ȱ������Σ�MN=t
���MFN=90�㣬FM=$\frac{\sqrt{3}}{2}$t��FN=$\frac{1}{2}$MN=$\frac{1}{2}$t��
��FE=$\frac{\sqrt{3}}{4}$t��
��S=S��FBN=$\frac{1}{2}•t•\frac{\sqrt{3}}{4}t$=$\frac{\sqrt{3}}{8}$t2��0��t��4����
��4��t��6ʱ����ͼ3��ʾ����HG��MN�ڵ�G
�ߡ�ABC=30�㣬��PMNΪ�ȱ������Σ�MN=t��
��BM=HM=t-4��HG=$\frac{\sqrt{3}}{2}$��t-4����
��S��HBM=$\frac{1}{2}$•��t-4��•$\frac{\sqrt{3}}{2}$��t-4��=$\frac{\sqrt{3}}{4}$��t-4��2
��S=S��FBN-S��HBM=$\frac{\sqrt{3}}{8}$t2-$\frac{\sqrt{3}}{4}$��t-4��2��4��t��6����
��6��t��8ʱ����ͼ4��ʾ��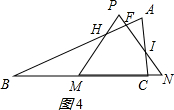
�ߡ�N=60�㣬NC=t-10��
��IC=$\sqrt{3}$��t-10����
��S��ICN=$\frac{1}{2}$•��t-10��•$\sqrt{3}$��t-10��=$\frac{\sqrt{3}}{2}$��t-10��2��
��S=S��FBN-S��HBM-S��ICN$\frac{\sqrt{3}}{8}$t2-$\frac{\sqrt{3}}{4}$��t-4��2-$\frac{\sqrt{3}}{2}$��t-10��2��6��t��8����
��8��t��10ʱ����ͼ3��ʾ��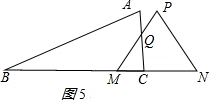
��BM=t-4����QMC=60�㣬
��MC=10-t��QC=$\frac{\sqrt{3}}{3}$��10-t����
��S=S��QMC=$\frac{1}{2}$•��10-t��•$\frac{\sqrt{3}}{3}$��10-t��=$\frac{\sqrt{3}}{6}$��10-t��2��8��t��10����
�۴��ڣ�����DEMΪ���������Σ���MӦ����DE�Ĵ�ֱƽ�����ϣ�
�ߵ�DΪAB���е㣬��EΪAC���е㣬
��DE=$\frac{1}{2}$BC=3��
���ʱMC=1.5
��t=8.5��
���� ���⿼�����������������ʡ�ֱ�����������ʡ��������������ʡ���ֱƽ�������ʣ�����Ĺؼ���Ҫ���з��������ҵ��ص�ͼ�������t��ȡֵ��Χ���������������ζ�Ӧ�߳ɱ����ҵ�����t�Ĺ�ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | ��m�й� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
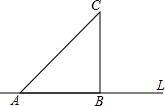 ��ͼ������ֱ��������ABC��һֱ�DZ�AB��ֱ��L�ϣ��������������Ŷ���B˳ʱ�뷽����ת������BC����ֱ��L�ϣ����ƶ���C˳ʱ����ת����CA����ֱ��L�ϣ���AB=1����A���˶��켣��ֱ��LΧ�ɵ�ͼ�ε�����Ǧ�+$\frac{1}{2}$��
��ͼ������ֱ��������ABC��һֱ�DZ�AB��ֱ��L�ϣ��������������Ŷ���B˳ʱ�뷽����ת������BC����ֱ��L�ϣ����ƶ���C˳ʱ����ת����CA����ֱ��L�ϣ���AB=1����A���˶��켣��ֱ��LΧ�ɵ�ͼ�ε�����Ǧ�+$\frac{1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������� | 10 | 50 | 100 | 200 | 500 | 1000 | 2000 |
| �¼�������Ƶ�� | 0.245 | 0.248 | 0.251 | 0.253 | 0.249 | 0.252 | 0.251 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com