
【题目】某公司共有![]() 三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.
三个部门,根据每个部门的员工人数和相应每人所创的年利润绘制成如下的统计表和扇形图.

各部门人数及每人所创年利润统计表
部门 | 员工人数 | 每人所创的年利润/万元 |
A | 5 | 10 |
B |
| 8 |
C |
| 5 |
(1)①在扇形图中,C部门所对应的圆心角的度数为___________;
②在统计表中,![]() ___________,
___________,![]() ___________;
___________;
(2)求这个公司平均每人所创年利润.
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() 的图象分别位于第二、第四象限,A(x1,y1)、B(x2,y2)两点在该图象上,下列命题:①过点A作AC⊥x轴,C为垂足,连接OA.若△ACO的面积为3,则k=﹣6;②若x1<0<x2,则y1>y2;③若x1+x2=0,则y1+y2=0,其中真命题个数是( )
的图象分别位于第二、第四象限,A(x1,y1)、B(x2,y2)两点在该图象上,下列命题:①过点A作AC⊥x轴,C为垂足,连接OA.若△ACO的面积为3,则k=﹣6;②若x1<0<x2,则y1>y2;③若x1+x2=0,则y1+y2=0,其中真命题个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
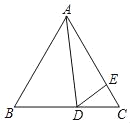
【题目】如图,等边△ABC中,D为BC边上一点,E为AC边上一点,∠ADE=60°
(1)求证:△ABD∽△DCE;
(2)若BD=4,CE=![]() ,求△ABC的边长.
,求△ABC的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
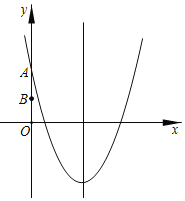
【题目】如图,抛物线y=![]() ﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.
﹣4x+4与y轴交于点A,B是OA的中点,一个动点G从点B出发,先经过x轴上的点M,再经过物线对称轴上的点N,然后返回到点A,则点G走过的最短路程为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
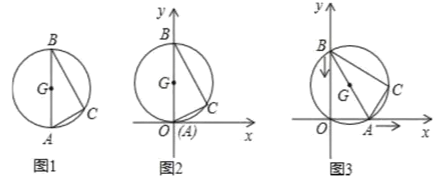
【题目】图1是用钢丝制作的一个几何探究工具,其中△ABC内接于⊙G,AB是⊙G的直径,AB=6,AC=2,现将制作的几何探究工具放在平面直角坐标系中(如图2),然后点A在射线OX上由点O开始向右滑动,点B在射线OY上也随之向点O滑动(如图3),当点B滑动至与点O重合时运动结束,在整个运动过程中,点C运动的路径长是( )
A.![]() πB.2πC.4
πB.2πC.4![]() -2D.10-4
-2D.10-4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
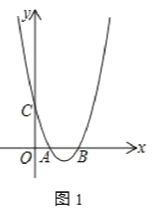
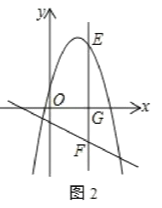
【题目】已知二次函数y=x2+bx+c,其图象抛物线交x轴于点A(1,0)、B(3,0),交 y轴于点C,直线l过点C,且交抛物线于另一点E(点E不与点A、B重合).
(1)直接写出二次函数的解析式;
(2)若直线l1经过抛物线顶点D,交x轴于点F,且l1∥l,则以点C、D、E、F为顶点的四边形能否为平行四边形,若能,求出点E的坐标;若不能,请说明理由;
(3)将此抛物线沿着y=2翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线y=-![]() x-1于点F,求
x-1于点F,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() 与双曲线
与双曲线![]()
![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() 作
作![]() 轴于点
轴于点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() ,连接
,连接![]() .
.
(Ⅰ)求![]() ,
,![]() 两点的坐标;
两点的坐标;
(Ⅱ)试探究直线![]() 与
与![]() 的位置关系并说明理由.
的位置关系并说明理由.
(Ⅲ)已知点![]() ,且
,且![]() ,
,![]() 在抛物线
在抛物线![]()
![]() 上,若当
上,若当![]() (其中
(其中![]() )时,函数
)时,函数![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
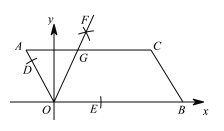
【题目】如图,已知平行四边形AOBC的顶点O(0,0),A(-3,4),点B在x轴正半轴上,按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于![]() DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
DE的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G.则点G的坐标为( )
A.(2,4)B.(5,4)C.(-2,4)D.(3,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
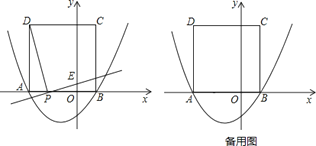
(1)请直接写出点D的坐标: ;
(2)当点P在线段AO(点P不与A、O重合)上运动至何处时,线段OE的长有最大值,求出这个最大值;
(3)是否存在这样的点P,使△PED是等腰三角形?若存在,请求出点P的坐标及此时△PED与正方形ABCD重叠部分的面积;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com