
【题目】在平面直角坐标系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三点,其中t>0,函数![]() 的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
的图象分别与线段BC,AC交于点P,Q.若S△PAB-S△PQB=t,则t的值为__.
科目:初中数学 来源: 题型:
【题目】为了了解某校学生对以下四个电视节目:![]() 最强大脑
最强大脑![]() 、
、![]() 中国诗词大会
中国诗词大会![]() 、
、![]() 朗读者
朗读者![]() 、
、![]() 出彩中国人
出彩中国人![]() 的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.
的喜爱情况,随机抽取了部分学生进行调查,要求每名学生选出并且只能选出一个自己最喜爱的节目,根据调查结果,绘制了如下两幅不完整的统计图.

请你根据图中所提供的信息,完成下列问题:
![]() 本次调查的学生人数为______;
本次调查的学生人数为______;
![]() 在扇形统计图中,A部分所占圆心角的度数为______;
在扇形统计图中,A部分所占圆心角的度数为______;
![]() 请将条形统计图补充完整;
请将条形统计图补充完整;
![]() 若该校共有3000名学生,估计该校最喜爱
若该校共有3000名学生,估计该校最喜爱![]() 中国诗词大会
中国诗词大会![]() 的学生有多少名.
的学生有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 是平行四边形,
是平行四边形,![]() ,若
,若![]() ,
,![]() 的长是关于
的长是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,且
的两个根,且![]() .
.

(1)直接写出:![]() ______,
______,![]() ______;
______;
(2)若点![]() 为
为![]() 轴正半轴上的点,且
轴正半轴上的点,且![]() ;
;
①求经过![]() ,
,![]() 两点的直线解析式;
两点的直线解析式;
②求证:![]() .
.
(3)若点![]() 在平面直角坐标系内,则在直线
在平面直角坐标系内,则在直线![]() 上是否存在点
上是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,直接写出
为顶点的四边形为菱形?若存在,直接写出![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
如图1.在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,可以得到:
![]()
证明:过点A作AD⊥BC,垂足为D.
在Rt△ABD中,![]()
∴![]()
∴![]()
同理:![]()
![]()
∴![]()
(1)通过上述材料证明:
![]()
(2)运用(1)中的结论解决问题:
如图2,在![]() 中,
中,![]() ,求AC的长度.
,求AC的长度.
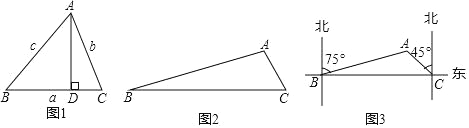
(3)如图3,为了开发公路旁的城市荒地,测量人员选择A、B、C三个测量点,在B点测得A在北偏东75°方向上,沿笔直公路向正东方向行驶18km到达C点,测得A在北偏西45°方向上,根据以上信息,求A、B、C三点围成的三角形的面积.
(本题参考数值:sin15°≈0.3,sin120°≈0.9,![]() ≈1.4,结果取整数)
≈1.4,结果取整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=3.
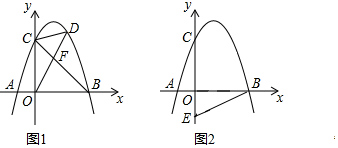
(1)求该抛物线的函数解析式;
(2)如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD,OD交BC于点F,当S△COF:S△CDF=3:2时,求点D的坐标.
(3)如图2,点E的坐标为(0,![]() ),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
),在抛物线上是否存在点P,使∠OBP=2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元
/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润.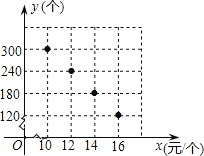
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形![]() ,
,![]() ,抛物线
,抛物线![]() 为常数),顶点为
为常数),顶点为![]() .
.
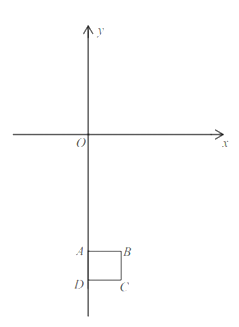
(1)拋物线经过定点坐标是___ __,顶点![]() 的坐标(用
的坐标(用![]() 的代数式表示)是____ _.
的代数式表示)是____ _.
(2)若抛物线![]() (
(![]() 为常数)与正方形
为常数)与正方形![]() 的边有交点,则
的边有交点,则![]() 的取值范围是___ _.
的取值范围是___ _.
(3)若![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 交x轴于A.B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(1,0).
交x轴于A.B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(1,0).
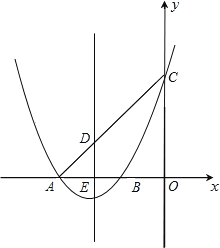
(1)求抛物线的对称轴及点A的坐标;
(2)连结CA与抛物线的对称轴交于点D.
①在对称轴上找一点P,使ΔAPC为直角三角形,求点P的坐标.
②在抛物线上是否存在点M,使得直线CM把四边形DEOC分成面积相等的两部分?若存在,请求出直线CM的解析式;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com