
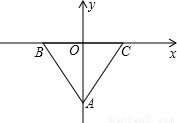
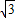 ,设OG的长度为y,则AG的长度为3
,设OG的长度为y,则AG的长度为3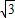 -y,根据时间等于路程除以速度,设电子虫在y轴上的速度为2v,则在GC上的速度为v,列出时间表达式,再根据不等式当且仅当
-y,根据时间等于路程除以速度,设电子虫在y轴上的速度为2v,则在GC上的速度为v,列出时间表达式,再根据不等式当且仅当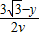 =
=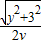 时取最小值,求出y值,点G坐标可得.
时取最小值,求出y值,点G坐标可得.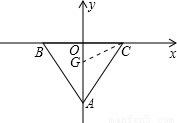 解:根据题意,AO=6sin60°=3
解:根据题意,AO=6sin60°=3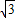 ,
,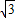 -y,
-y,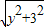 ,
,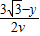 +
+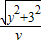 ,
,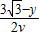 =
=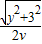 时,t有最小值,
时,t有最小值,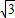 -y=2
-y=2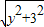 ,
,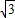 y+3=0,
y+3=0,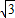 .
.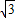 ).
).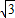 ).
).

科目:初中数学 来源: 题型:
 线段MN运动的时间为t秒.
线段MN运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:
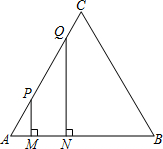
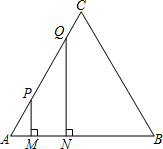 如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )
如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )A、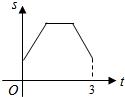 | B、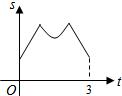 | C、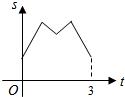 | D、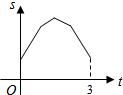 |
查看答案和解析>>
科目:初中数学 来源: 题型:
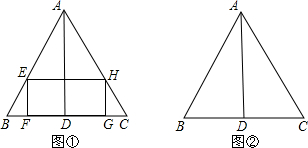
查看答案和解析>>
科目:初中数学 来源: 题型:
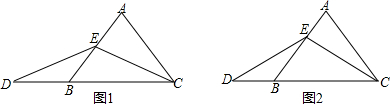
查看答案和解析>>
科目:初中数学 来源:2009年江苏省无锡市北塘区中考数学二模试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com