
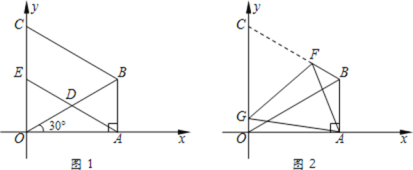
【题目】如图1,在△ABO中,∠OAB=90°,∠AOB=30°,OB=8.以OB为一边,在△OAB外作等边三角形OBC,D是OB的中点,连接AD并延长交OC于E.
(1)求点B的坐标;
(2)求证:四边形ABCE是平行四边形;
(3)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.
【答案】(1)(4![]() ,4);(2)见解析;(3)1.
,4);(2)见解析;(3)1.
【解析】
(1)由在△ABO中,∠OAB=90°,∠AOB=30°,OB=8,根据勾股定理即可求得AB与OA的长,即可求得点B的坐标;
(2)首先可得CE∥AB,D是OB的中点,根据直角三角形斜边的中线等于斜边的一半,可证得BD=AD,∠ADB=60°,又由△OBC是等边三角形,可得∠ADB=∠OBC,根据内错角相等,两直线平行,可证得BC∥AE,继而可得四边形ABCD是平行四边形;
(3)首先设OG的长为x,由折叠的性质可得:AG=CG=8-x,然后根据勾股定理可得方程(8-x)2=x2+(4![]() )2,解此方程即可求得OG的长.
)2,解此方程即可求得OG的长.
在△OAB中,∠OAB=90°,∠AOB=30°,OB=8,
∴AB=![]() OB=
OB=![]() ×8=4,
×8=4,
OA=OB-AB
∴OA= ![]() =
=![]() =4
=4![]()
∴点B的坐标为(4![]() ,4);
,4);
(2)证明:∵∠OAB=90°,
∴AB⊥x轴,
∵y轴⊥x轴,
∴AB∥y轴,即AB∥CE,
∵∠AOB=30°,
∴∠OBA=60°,
∵DB=DO=4
∴DB=AB=4
∴∠BDA=∠BAD=120°÷2=60°,
∴∠ADB=60°,
∵△OBC是等边三角形,
∴∠OBC=60°,
∴∠ADB=∠OBC,
即AD∥BC,
∴四边形ABCE是平行四边形;
(3)设OG的长为x,
∵OC=OB=8,
∴CG=8﹣x,
由折叠的性质可得:AG=CG=8﹣x,
在Rt△AOG中,AG2=OG2+OA2,
即(8﹣x)2=x2+(4![]() )2,
)2,
解得:x=1,
即OG=1.


 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,AB=AC,∠ABC的平分线BD交AC于点D,CE⊥BD,交BD的延长线于点E,若BD=6,则CE的值为( )
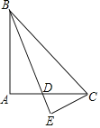
A. 4B. 3.5C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
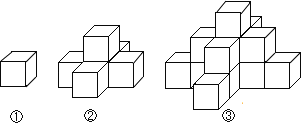
【题目】如图①是一个水平放置的小正方体木块,图②、图③是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,第四个叠放的图形时,小正方体木块总数应是___块;第七个叠放的图形时,小正方体木块总数应是____块.
查看答案和解析>>
科目:初中数学 来源: 题型:
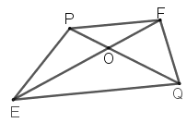
【题目】如图 ,等腰三角形PEF中,PE=PF,点O在EF边上(异于点E,F),点Q是PO延长线上一点,若△EFQ为等腰三角形,则称点Q为△PEF的“同类点”.
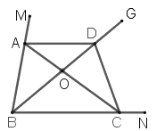
(1)如图,BG平分∠MBN,过射线BM上的点A作AD∥BN,交射线BG于点D,点O为BD上一点,连接AO并延长交射线BN于点C,若∠BAD=100°,∠BCD=70°,求证:点C是△ABD的“同类点”;
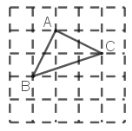
(2)如图③,在5×5的正方形网格图上有一个△ABC,点A,B,C均在格点上,在给出的网格图上有一个格点D,使得点D为△ABC的“同类点”,则这样的点D共有__________个;
(3)凸四边形ABCD中,∠ABC=110°,DA=AB=BC,对角线AC,BD交于点O,且BD≠CD,若点C为△ABD的“同类点”,请直接写出满足条件的∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:
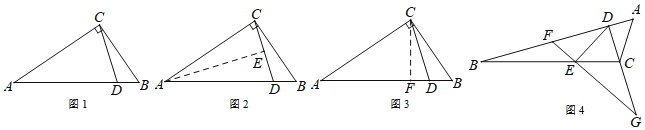
如图1,△ABC中,∠ACB=90°,点D在AB上,且∠BAC=2∠DCB,求证:AC=AD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法1:如图2,作AE平分∠CAB,与CD相交于点E.
方法2:如图3,作∠DCF=∠DCB,与AB相交于点F.
(1)根据阅读材料,任选一种方法,证明AC=AD.
用学过的知识或参考小明的方法,解决下面的问题:
(2)如图4,△ABC中,点D在AB上,点E在BC上,且∠BDE=2∠ABC,点F在BD上,且∠AFE=∠BAC,延长DC、FE,相交于点G,且∠DGF=∠BDE.
①在图中找出与∠DEF相等的角,并加以证明;
②若AB=kDF,猜想线段DE与DB的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
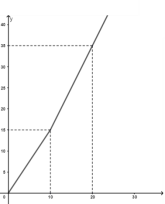
【题目】我国是世界上严重缺水的国家之一。为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费。即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费。设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示。
(1)求a的值;某户居民上月用水8吨,应收水费多少元?
(2)求b的值,并写出当x>10时,y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4吨,两家共收水费46元,求他们上月分别用水多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行了一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分成四类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
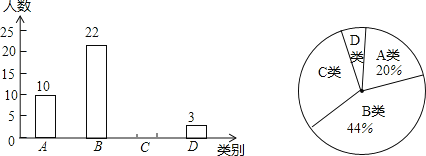
(1)求本次抽取的样本容量和扇形统计图中A类所对的圆心角的度数;
(2)若该校九年级男生有500名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上![]() ,
,![]() 两点对应的有理数分别为
两点对应的有理数分别为![]() 和12,点
和12,点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿数轴负方向运动,点
出发,以每秒1个单位长度的速度沿数轴负方向运动,点![]() 同时从点
同时从点![]() 出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为
出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为![]() 秒.
秒.
![]()
(1)求经过2秒后,数轴点![]() 、
、![]() 分别表示的数;
分别表示的数;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在运动过程中是否存在时间![]() 使
使![]() ,若存在,请求出此时
,若存在,请求出此时![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
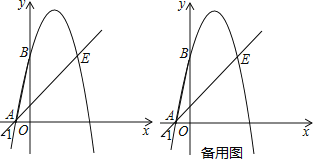
【题目】如图,抛物线y=ax2+4x+c(a≠0)经过点A(﹣1,0),点E(4,5),与y轴交于点B,连接AB.
(1)求该抛物线的解析式;
(2)将△ABO绕点O旋转,点B的对应点为点F.
①当点F落在直线AE上时,求点F的坐标和△ABF的面积;
②当点F到直线AE的距离为![]() 时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
时,过点F作直线AE的平行线与抛物线相交,请直接写出交点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com