
 2015��9��7�պӱ����걨��������Ի�����������������������ͣ���ѵ����⣬ס���ͳ��罨�趼���������мӿ���Ƴ���ͣ����ʩר��滮���������ͣ��ì�ܣ�ij�����̳�ǰ�п鳤���οյأ����̳��ƻ����˿�յ�����ͣ�����������ͼ��ͼ��ʾ����Ӱ����Ϊͣ��λ������С��Ӱ���ֵ������ȣ��հײ���Ϊ�����������Ŀ���ȣ�
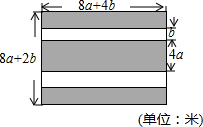
2015��9��7�պӱ����걨��������Ի�����������������������ͣ���ѵ����⣬ס���ͳ��罨�趼���������мӿ���Ƴ���ͣ����ʩר��滮���������ͣ��ì�ܣ�ij�����̳�ǰ�п鳤���οյأ����̳��ƻ����˿�յ�����ͣ�����������ͼ��ͼ��ʾ����Ӱ����Ϊͣ��λ������С��Ӱ���ֵ������ȣ��հײ���Ϊ�����������Ŀ���ȣ����� ��1������ͼ�κ���Ŀ�е���Ϣ�����ú�a��b��ʽ�ӱ�ʾͣ��λ���������
��2������ͣ�����ij��Ϳ��Լ�ÿ��ͣ��λ�Ŀ�Ϊ2.4�ף���Ϊ5.5�ף�������ø��̳��ƻ�����ͣ�����ij�λ����
��� �⣺��1��������ɵã�
��Ӱ���ֵ����Ϊ����8a+4b����8a+2b-2b��=��64a2+32ab��ƽ���ף�
��ͣ��λ�������Ϊ��64a2+32ab��ƽ���ף�
��2��������ɵã�
��a=2.5��b=4ʱ��
ͣ�����ij�Ϊ��8a+4b=8��2.5+4��4=36�ף�
����̳��ƻ�����ͣ�����ij�λ��Ϊ��36��2.4��4=60��
�����̳��ƻ�����ͣ�����ij�λ��Ϊ60��
���� ���⿼����ʽ�Ļ�����㡢����ʽ��ֵ������Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ���������������ν�ϵ�˼����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 16 | B�� | 3 | C�� | ��3 | D�� | 14 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3-2$\sqrt{3}$ | B�� | 0 | C�� | 8-4$\sqrt{3}$ | D�� | 8+4$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� |  | B�� |  | ||
| C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��1����2����4�� | B�� | ��4����2����3�� | C�� | ��1����2����3�� | D�� | ��4����1����2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ABC�У�AD��BC��D����BA=CA������Ƴ���ABD�ա�ACD���������ǣ�������
��ͼ����ABC�У�AD��BC��D����BA=CA������Ƴ���ABD�ա�ACD���������ǣ�������| A�� | AAS | B�� | ASA | C�� | SAS | D�� | HL |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ����ʽ | x | -$\frac{x}{2}$ | 8x2 | -$\frac{xyz}{3}$ | -$\frac{3}{5}$x2yz3 |
| ���� | 1 | 1 | 2 | 3 | 6 |
| ϵ�� | 1 | -$\frac{1}{2}$ | 8 | -$\frac{1}{3}$ | -$\frac{3}{5}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com