
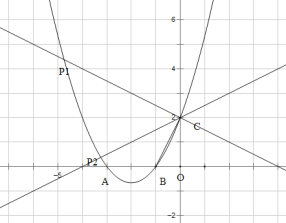
【题目】已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式.
(2)连接BC,求∠BCO的余切值.
(3)如果过点C的直线,交x轴于点E,交抛物线于点P,且∠CEO =∠BCO,求点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点P坐标是(
;(3)点P坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)首先设抛物线的解析式,然后根据对称轴和所经过的点,列出方程,即可得出解析式;
(2)首先求出B坐标,即可得出![]() ,
,![]() ,进而得出∠BCO的余切值;
,进而得出∠BCO的余切值;
(3)首先根据![]() 的余切值列出等式,得出点E的坐标,然后根据点C的坐标得出直线解析式,最后联立直线和抛物线的解析式即可得出点P坐标.
的余切值列出等式,得出点E的坐标,然后根据点C的坐标得出直线解析式,最后联立直线和抛物线的解析式即可得出点P坐标.
(1)设抛物线的表达式为![]() .
.
由题意得: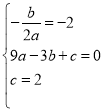
解得:![]() ,
,![]() .
.
∴这条抛物线的表达式为![]() .
.
(2)令y = 0,那么![]() ,
,
解得![]() ,
,![]() .
.
∵点A的坐标是(![]() 3,0)
3,0)
∴点B的坐标是(![]() 1,0).
1,0).
∵C(0,2)
∴![]() ,
,![]() .
.
在Rt△ OBC中,∠BOC=90,
∴![]() .
.
(3)设点E的坐标是(x,0),得OE=![]() .
.
∵![]() ,
,
∴![]() .
.
在Rt△EOC中,∴![]() .
.
∴![]() =4,∴点E坐标是(4,0)或 (
=4,∴点E坐标是(4,0)或 (![]() 4,0).
4,0).
∵点C坐标是(0,2),
∴![]() .
.
∴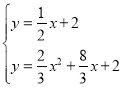 ,或
,或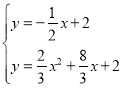
解得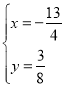 和
和![]() (舍去),或
(舍去),或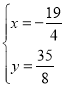 和
和![]() (舍去);
(舍去);
∴点P坐标是(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】某体育看台侧面的示意图如图所示,观众区![]() 的坡度为
的坡度为![]() ,顶端
,顶端![]() 离水平地面
离水平地面![]() 的高度为
的高度为![]() ,从顶棚的
,从顶棚的![]() 处看
处看![]() 处的仰角
处的仰角![]() ,竖直的立杆上
,竖直的立杆上![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 处到观众区底端
处到观众区底端![]() 处的水平距离
处的水平距离![]() 为
为![]() .求:
.求:
(1)观众区的水平宽度![]() ;
;
(2)顶棚的![]() 处离地面的高度
处离地面的高度![]() .(
.(![]() ,
,![]() ,结果精确到
,结果精确到![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
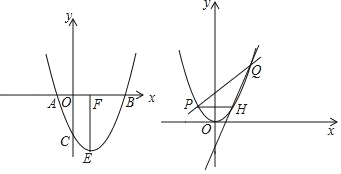
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
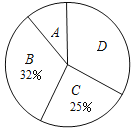
【题目】在“书香校园”活动中,某校为了解学生家庭藏书情况,随机抽取本校部分学生进行调查,并绘制成部分统计图表如下:
类别 | 家庭藏书m本 | 学生人数 |
A | 0≤m≤25 | 20 |
B | 26≤m≤50 | a |
C | 51≤m≤75 | 50 |
D | m≥76 | 66 |
根据以上信息,解答下列问题:
(1)该调查的样本容量为 ,a= ;
(2)随机抽取一位学生进行调查,刚好抽到A类学生的概率是 ;
(3)若该校有2000名学生,请估计全校学生中家庭藏书不少于76本的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
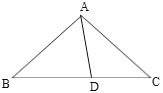
【题目】如图,在等腰△ABC中,AB=AC=4,BC=6点D在底边BC上,且∠DAC=∠ACD,将△ACD沿着AD所在直线翻折,使得点C落到点E处,联结BE,那么BE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
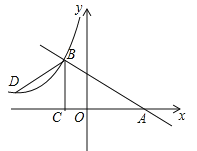
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有4个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4.
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率;
(2)随机摸出两个小球,直接写出“两次取出的球标号和为奇数”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,六个完全相同的小长方形拼成了一个大长方形,AB是其中一个小长方形的对角线,请在大长方形中完成下列画图,要求:①仅用无刻度直尺,②保留必要的画图痕迹.
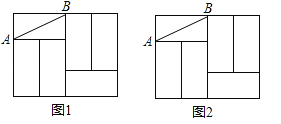
(1)在图1中画出一个45°角,使点A或点B是这个角的顶点,且AB为这个角的一边;
(2)在图2中画出线段AB的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
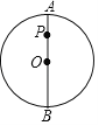
【题目】如图,AB是⊙O的直径,点P是AB上一点,且点P是弦CD的中点.
(1)依题意画出弦CD,并说明画图的依据;(不写画法,保留画图痕迹)
(2)若AP=2,CD=8,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com